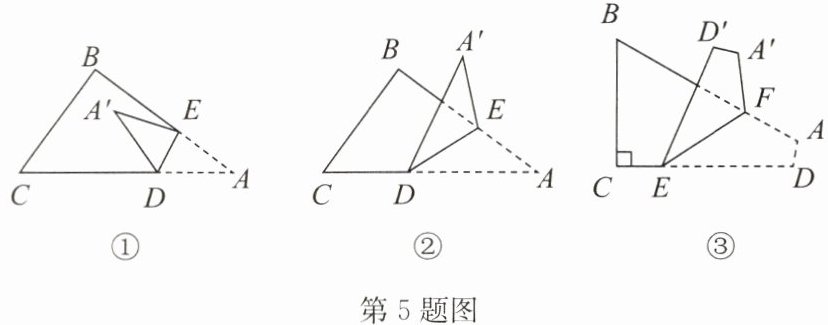
5. (1)如图①, 将$\triangle ABC$纸片沿 DE 折叠, 使点 A 落在四边形 BCDE 内点$A'$的位置, 则$∠A,∠A'DC,∠A'EB$之间的数量关系为____;
(2)如图②, 若将(1)“中点 A 落在四边形 BCDE 内点$A'$的位置”变为“点 A 落在四边形 BCDE 外点$A'$的位置”, 则此时$∠A,∠A'DC,∠A'EB$之间的数量关系为____;
(3)如图③, 将四边形 ABCD 纸片($∠C= 90^{\circ }$, AB 与 CD 不平行)沿 EF 折叠, 若$∠D'EC= 115^{\circ },∠A'FB= 45^{\circ }$, 求$∠B$的度数;
(4)在图③中作出$∠D'EC,∠A'FB$的平分线 EG,FH, 试判断射线 EG 与 FH 的位置关系, 当点 E 在 DC 边上向点 C 移动时(不与点 C 重合),$∠D'EC,∠A'FB$的大小随之改变(其他条件不变), 上述 EG 与 FH 的位置关系会改变吗? 为什么?
答案:(1)2∠A = ∠A'DC + ∠A'EB
(2)2∠A = ∠A'DC − ∠A'EB
(3)解:如答图①,延长BA,CD交于点Q,延长ED',FA'交于点Q',
∴折叠后的△EFQ与△EFQ'重合
由
(2)的结论可得:2∠Q = ∠D'EC − ∠A'FB,而∠D'EC = 115°,∠A'FB = 45°,
∴2∠Q = 115° − 45° = 70°,
∴∠Q = 35°,
∵∠C = 90°,
∴∠B = 90° − 35° = 55°.

(4)解:EG//FH,不会改变.理由:
如答图②,EG平分∠D'EC,FH平分∠A'FB,
∴∠D'EG = ∠CEG = $\frac{1}{2}$∠D'EC,∠A'FH = ∠BFH = $\frac{1}{2}$∠A'FB.
由折叠可得:∠Q'EF = ∠QEF,∠Q'FE = ∠QFE;
由
(2)的结论可得:∠D'EC − ∠A'FB = 2∠Q,
即∠D'EC = ∠A'FB + 2∠Q,
∴∠D'EG = ∠A'FH + ∠Q,
∴∠D'EG + ∠D'EF + ∠BFE + ∠BFH = ∠A'FH + ∠Q + ∠QEF + ∠BFH + ∠BFE,
∴∠FEG + ∠HFE = ∠Q + ∠QEF + ∠Q'FE,
∴∠FEG + ∠HFE = ∠Q + ∠QEF + ∠QFE = 180°,
∴EG//FH.
6. 【问题呈现】(1)如图①, 在$\triangle ABC$中,$∠C>∠B$, AE 平分$∠BAC,AD⊥BC$于点 D, 猜想$∠B,∠C,∠EAD$之间的数量关系;

答案:解:
∵∠BAC = 180° − ∠B − ∠C,∠BAE = $\frac{1}{2}$∠BAC,∠BAD = 90° − ∠B,
∴∠EAD = ∠BAD − ∠BAE = 90° − ∠B − $\frac{1}{2}$(180° − ∠B − ∠C) = 90° − ∠B − 90° + $\frac{1}{2}$∠B + $\frac{1}{2}$∠C = $\frac{1}{2}$(∠C − ∠B),
∴∠EAD = $\frac{1}{2}$(∠C − ∠B).
【变式应用】(2)在图②中,$∠B= 35^{\circ },∠C= 75^{\circ }$, 其余条件不变, 若把“$AD⊥BC$于点 D”改为“F 是线段 AE 上一点,$FD⊥BC$于点 D”, 求$∠DFE$的度数, 并写出$∠DFE与∠B,∠C$之间的数量关系;
【思维发散】(3)交换 B,C 两个字母的位置, 在图③中, 若把(2)中的“点 F 在线段 AE 上”改为“F 是 EA 延长线上一点”, 其余条件不变, 当$∠ABC= 88^{\circ },∠C= 24^{\circ }$时,$∠F$的度数为____$^{\circ }$;
【能力提升】(4)在图④中, 若点 F 在 AE 的延长线上,$FD⊥BC$于点 D, 设$∠B= x,∠C= y$, 其余条件不变, 分别作出$∠CAE和∠EDF$的平分线, 交于点 P, 试用含 x,y 的代数式表示$∠P$, 则$∠P= $____.
答案:(2)解:如答图,过点A作AG⊥BC于点G.

∵FD⊥BC,AG⊥BC,
∴FD//AG,
∴∠DFE = ∠EAG.
∵∠B = 35°,∠C = 75°,
由
(1)同理可得:∠EAG = $\frac{1}{2}$(∠C − ∠B) = $\frac{1}{2}$(75° − 35°) = 20°,
∴∠DFE = ∠EAG = 20°.
(3)32
(4)$\frac{1}{4}$(3y - x)