2025年启东中学作业本八年级数学上册人教版第13页解析答案

4. (2024春·仪征期末)如图是可调躺椅示意图(数据如图),$AE与BD的交点为C$,且$\angle CAB$、$\angle CBA$、$\angle D$的大小保持不变. 为了舒适,需调整$\angle E$的大小,使$\angle EFD= 110^{\circ}$,则图中$\angle E$应 (

)

A.增加$10^{\circ}$
B.减少$10^{\circ}$
C.增加$20^{\circ}$
D.减少$20^{\circ}$

答案：B

解析：

在$\triangle ABC$中，$\angle CAB=50^\circ$，$\angle CBA=60^\circ$，则$\angle ACB=180^\circ - 50^\circ - 60^\circ=70^\circ$。
$\angle DCE=\angle ACB=70^\circ$（对顶角相等）。
在$\triangle CDE$中，$\angle D=20^\circ$，则$\angle E=180^\circ - \angle DCE - \angle D=180^\circ - 70^\circ - 20^\circ=90^\circ$。
$\angle EFD$是$\triangle DFC$的外角，$\angle D=20^\circ$，$\angle DCF=180^\circ - \angle ACB=110^\circ$，所以$\angle EFD=\angle D + \angle DCF=20^\circ + 110^\circ=130^\circ$。
要使$\angle EFD=110^\circ$，需$\angle EFD$减少$130^\circ - 110^\circ=20^\circ$，则$\angle E$应减少$10^\circ$。
B

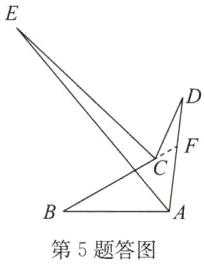
5. (1)如图①,$\angle BAD的平分线AE与\angle BCD的平分线CE交于点E$,$AB// CD$,$\angle D= 40^{\circ}$,$\angle B= 30^{\circ}$,求$\angle E$的大小.
(2)如图②,$\angle BAD的平分线AE与\angle BCD的平分线CE交于点E$,$\angle D= m^{\circ}$,$\angle B= n^{\circ}$,求$\angle E$的大小.
(3)如图③,$\angle BAD的平分线AE与\angle BCD的平分线CE交于点E$,则$\angle E与\angle D$、$\angle B$之间是否仍存在某种等量关系？若存在,请写出你的结论,并给出证明；若不存在,请说明理由.

答案：
5.解:
(1)
∵CE平分∠BCD,AE平分∠BAD,
∴∠ECD=∠ECB=$\frac{1}{2}$∠BCD,∠EAD=∠EAB=$\frac{1}{2}$∠BAD.
∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E +∠ECB,
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB,
∴∠D+∠B=2∠E,
∴∠E=$\frac{1}{2}$(∠D+∠B).
∵∠D=40°,∠B=30°,
∴∠E=$\frac{1}{2}$×(40°+30°)=35°.
(2)由
(1)同理易得,∠E=$\frac{1}{2}$(∠D+∠B),
∵∠D=m°,∠B=n°,
∴∠E=$\frac{m°+n°}{2}$.
(3)存在.∠E=$\frac{∠B-∠D}{2}$.
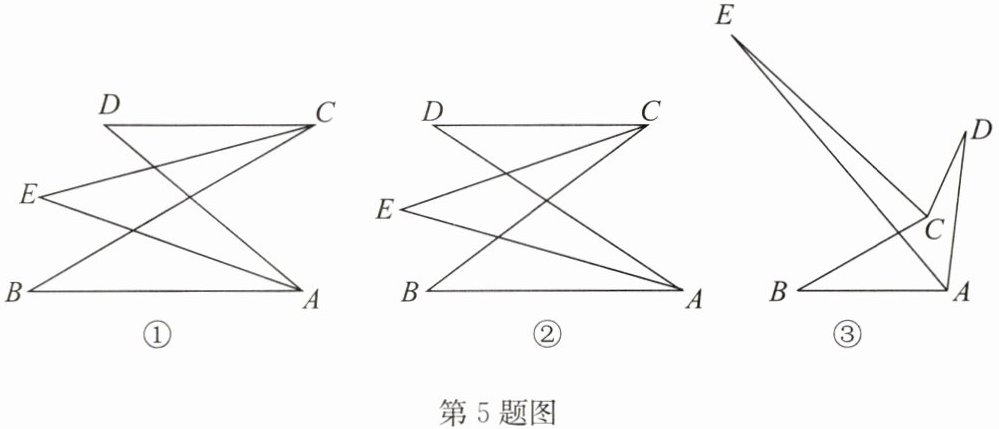
　证明如下:延长BC交AD于点F,如答图,
∵∠BFD=∠B+∠BAD,
∴∠BCD=∠BFD+∠D=∠B+∠BAD+∠D.
∵CE平分∠BCD,AE平分∠BAD,
∴∠ECD=∠ECB=$\frac{1}{2}$∠BCD,∠EAD=∠EAB=$\frac{1}{2}$∠BAD.
∵∠E+∠ECB=∠B+∠EAB,
∴∠E=∠B+∠EAB-∠ECB=∠B+∠EAB-$\frac{1}{2}$∠BCD=∠B+∠EAB-$\frac{1}{2}$(∠B+∠BAD+∠D)=$\frac{1}{2}$(∠B-∠D),即∠E=$\frac{∠B-∠D}{2}$.
　　　　　　