2025年启东中学作业本八年级数学上册人教版第12页解析答案

1. 如图,在$\triangle ABC$中,$BD$,$CD分别平分\angle ABC$,$\angle ACB$,$BG$,$CG分别平分\triangle ABC的两个外角\angle EBC$,$\angle FCB$,则$\angle D和\angle G$的数量关系为 (

)

A.$\angle D= \frac{1}{2}\angle G$
B.$\angle D+\angle G= 180^{\circ}$
C.$\angle D+\frac{1}{2}\angle G= 90^{\circ}$
D.$\angle D= 90^{\circ}+\frac{1}{2}\angle G$

答案：B

解析：

在$\triangle ABC$中，$\angle ABC + \angle ACB = 180^\circ - \angle A$。
$\because BD, CD$分别平分$\angle ABC, \angle ACB$，
$\therefore \angle DBC = \frac{1}{2}\angle ABC, \angle DCB = \frac{1}{2}\angle ACB$，
$\angle D = 180^\circ - (\angle DBC + \angle DCB) = 180^\circ - \frac{1}{2}(\angle ABC + \angle ACB) = 180^\circ - \frac{1}{2}(180^\circ - \angle A) = 90^\circ + \frac{1}{2}\angle A$。
$\because \angle EBC, \angle FCB$是$\triangle ABC$的外角，
$\therefore \angle EBC = 180^\circ - \angle ABC, \angle FCB = 180^\circ - \angle ACB$，
$\angle EBC + \angle FCB = 360^\circ - (\angle ABC + \angle ACB) = 360^\circ - (180^\circ - \angle A) = 180^\circ + \angle A$。
$\because BG, CG$分别平分$\angle EBC, \angle FCB$，
$\therefore \angle GBC = \frac{1}{2}\angle EBC, \angle GCB = \frac{1}{2}\angle FCB$，
$\angle G = 180^\circ - (\angle GBC + \angle GCB) = 180^\circ - \frac{1}{2}(\angle EBC + \angle FCB) = 180^\circ - \frac{1}{2}(180^\circ + \angle A) = 90^\circ - \frac{1}{2}\angle A$。
$\angle D + \angle G = (90^\circ + \frac{1}{2}\angle A) + (90^\circ - \frac{1}{2}\angle A) = 180^\circ$。
B

2. 如图,在$\triangle ABC$中,$BO$,$CO分别平分\angle ABC$,$\angle ACB$,交于点$O$,$CE为外角\angle ACD$的平分线,$BO的延长线交CE于点E$,记$\angle BAC= \angle 1$,$\angle BEC= \angle 2$,则以下结论：①$\angle 1= 2\angle 2$,②$\angle BOC= 3\angle 2$,③$\angle BOC= 90^{\circ}+\angle 1$,④$\angle BOC= 90^{\circ}+\angle 2$中,正确的是 (

)

A.①②③
B.①③④
C.①④
D.①②④

答案：C

解析：

∵BO平分∠ABC，CE平分∠ACD，
∴∠ABC=2∠EBC，∠ACD=2∠ECD，
∵∠ACD=∠ABC+∠1，∠ECD=∠EBC+∠2，
∴2∠ECD=2∠EBC+2∠2，
即∠ACD=∠ABC+2∠2，
∴∠1=2∠2，①正确；
∵BO、CO分别平分∠ABC、∠ACB，
∴∠OBC=$\frac{1}{2}$∠ABC，∠OCB=$\frac{1}{2}$∠ACB，
∠BOC=180°-∠OBC-∠OCB=180°-$\frac{1}{2}$(∠ABC+∠ACB)，
∵∠ABC+∠ACB=180°-∠1，
∴∠BOC=180°-$\frac{1}{2}$(180°-∠1)=90°+$\frac{1}{2}$∠1，
又∠1=2∠2，
∴∠BOC=90°+∠2，④正确，③错误；
假设∠BOC=3∠2，则90°+∠2=3∠2，∠2=45°，∠1=90°，
但∠1不一定为90°，故②错误。
综上，正确的是①④，选C。

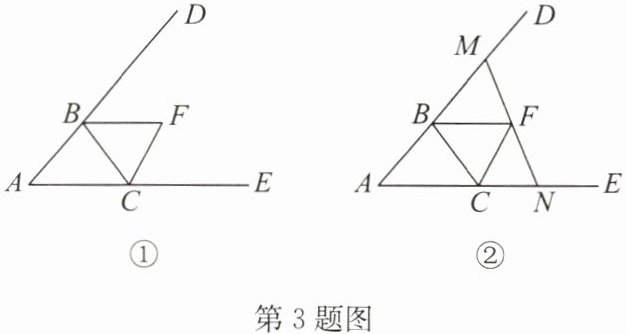
3. 如图①,$\triangle ABC的外角平分线BF$,$CF交于点F$.
(1)若$\angle A= 50^{\circ}$,则$\angle F$的度数为______.
(2)过点$F作直线MN$,分别交射线$AB$,$AC于点M$,$N$,并将直线$MN绕点F$旋转.
①如图②,当直线$MN与线段BC$没有交点时,若设$\angle MFB= \alpha$,$\angle NFC= \beta$,试探索$\angle A与\alpha$,$\beta$之间满足的数量关系,并说明理由.
②当直线$MN与线段BC$有交点时,试问①中$\angle A与\alpha$,$\beta$之间的数量关系是否仍然成立？若成立,请说明理由；若不成立,请求出三者之间满足的数量关系.

答案：
3.
(1)65°
(2)解:①α+β-$\frac{1}{2}$∠A=90°.理由:由
(1)可知∠BFC=90°-$\frac{1}{2}$∠A,∠MFB=α,∠NFC=β.
∵∠BFC+∠MFB+∠NFC=180°,
∴α+β+90°-$\frac{1}{2}$∠A=180°,
∴α+β-$\frac{1}{2}$∠A=90°.
　②不成立.如答图,
　　　　　　　　

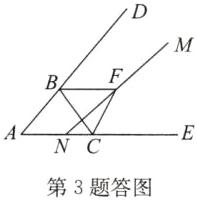
　由
(1)可知∠BFC=90°-$\frac{1}{2}$∠A,∠MFB=α,∠NFC=β.
∵∠BFN+∠NFC=∠BFC,
∴∠BFN=90°-$\frac{1}{2}$∠A-β.
∵∠BFN+∠MFB=180°,
∴90°-$\frac{1}{2}$∠A-β+α=180°,
∴α-β-$\frac{1}{2}$∠A=90°.