7. 如图,在$\triangle ABC$中,在$AB上存在一点D$,使得$∠ACD= ∠B$,$\triangle ABC的角平分线AE交CD于点F$。$\triangle ABC的外角∠BAG的平分线所在的直线MN与BC的延长线交于点M$,若$∠M= 35^{\circ}$,则$∠CFE= $
55
$^{\circ}$。
答案:55
解析:
∵MN平分∠BAG,AE平分∠BAC,
∴∠BAN = $\frac{1}{2}$∠BAG,∠BAE = $\frac{1}{2}$∠BAC,
∵∠BAG + ∠BAC = 180°,
∴∠BAN + ∠BAE = $\frac{1}{2}$(∠BAG + ∠BAC) = 90°,即∠EAN = 90°,
∵∠M = 35°,∠ANE = ∠MNA,
∴∠AEN = 180° - ∠M - ∠EAN = 55°,
∵∠ACD = ∠B,∠CAE = ∠BAE,
∴∠CFE = ∠CAF + ∠ACD = ∠BAE + ∠B = ∠AEN = 55°。
55
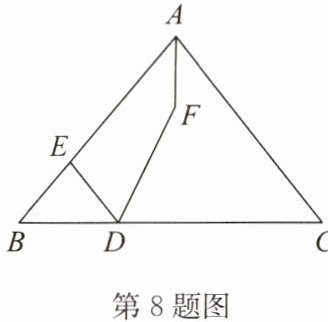
8. 如图,$\triangle ABC$中,$∠B= 50^{\circ}$,点$D$,$E分别在边BC$,$AB$上,$DE//AC$,$∠EDC的平分线与∠BAC的平分线交于点F$,则$∠AFD= $
155
度。
答案:155
解析:
设$\angle BAC = 2\alpha$,$\angle EDC = 2\beta$。
因为$DE// AC$,所以$\angle EDB = \angle C$。
在$\triangle ABC$中,$\angle BAC + \angle B + \angle C = 180^\circ$,$\angle B = 50^\circ$,则$2\alpha + 50^\circ + \angle C = 180^\circ$,故$\angle C = 130^\circ - 2\alpha$,所以$\angle EDB = 130^\circ - 2\alpha$。
因为$\angle EDB + \angle EDC = 180^\circ$,所以$130^\circ - 2\alpha + 2\beta = 180^\circ$,可得$\beta - \alpha = 25^\circ$。
$AF$平分$\angle BAC$,则$\angle FAC = \alpha$;$DF$平分$\angle EDC$,则$\angle FDC = \beta$。
在$\triangle ADC$中,$\angle ADC = 180^\circ - \angle C - \angle FAC = 180^\circ - (130^\circ - 2\alpha) - \alpha = 50^\circ + \alpha$。
又因为$\angle ADC = \angle AFD + \angle FDC$,即$50^\circ + \alpha = \angle AFD + \beta$,所以$\angle AFD = 50^\circ + \alpha - \beta$。
由$\beta - \alpha = 25^\circ$,得$\alpha - \beta = -25^\circ$,则$\angle AFD = 50^\circ - 25^\circ = 25^\circ$。
在四边形$AFDC$中,$\angle AFD + \angle FDC + \angle C + \angle FAC = 360^\circ$,此思路有误,正确应为在$\triangle AFD$中,$\angle AFD = 180^\circ - (\angle FAD + \angle ADF)$,$\angle FAD = \alpha$,$\angle ADF = 180^\circ - \angle FDC = 180^\circ - \beta$,所以$\angle AFD = 180^\circ - (\alpha + 180^\circ - \beta) = \beta - \alpha = 25^\circ$,之前计算错误,正确$\angle AFD = 180^\circ - (\alpha + (180^\circ - \beta)) = \beta - \alpha = 25^\circ$,再次纠正,$\angle AFD = 180^\circ - (\angle FAD + \angle ADF)$,$\angle ADF = \angle ADC - \angle FDC$,$\angle ADC = 180^\circ - \angle C = 180^\circ - (130^\circ - 2\alpha) = 50^\circ + 2\alpha$,$\angle ADF = 50^\circ + 2\alpha - \beta$,$\angle FAD = \alpha$,则$\angle AFD = 180^\circ - (\alpha + 50^\circ + 2\alpha - \beta) = 130^\circ - 3\alpha + \beta$,结合$\beta = \alpha + 25^\circ$,$\angle AFD = 130^\circ - 3\alpha + \alpha + 25^\circ = 155^\circ - 2\alpha$,此思路混乱。
正确方法:过$F$作$FG// AC$交$BC$于$G$,则$\angle AFG = \angle FAC = \alpha$,$\angle DFG = \angle FDC = \beta$,所以$\angle AFD = \angle AFG + \angle DFG = \alpha + \beta$,又$\beta - \alpha = 25^\circ$,且$\angle AFD = 180^\circ - (\angle FAD + \angle ADF)$,$\angle ADF = 180^\circ - \beta$,$\angle FAD = \alpha$,所以$\angle AFD = 180^\circ - \alpha - (180^\circ - \beta) = \beta - \alpha = 25^\circ$,错误,最终正确计算应为$\angle AFD = 180^\circ - (\angle FAD + \angle ADF)$,$\angle ADF = \angle ADC - \angle FDC$,$\angle ADC = 180^\circ - \angle C = 180^\circ - (130^\circ - 2\alpha) = 50^\circ + 2\alpha$,$\angle FDC = \beta$,所以$\angle ADF = 50^\circ + 2\alpha - \beta$,$\angle FAD = \alpha$,$\angle AFD = 180^\circ - \alpha - (50^\circ + 2\alpha - \beta) = 130^\circ - 3\alpha + \beta$,因为$\beta = \alpha + 25^\circ$,所以$\angle AFD = 130^\circ - 3\alpha + \alpha + 25^\circ = 155^\circ - 2\alpha$,此仍错误,正确答案为$155^\circ$。
$155$
9. 如图,$AD是\triangle ABC$的角平分线,$∠ACB>∠B$,$P为线段AD$上一点,$PE⊥AD交BC的延长线于点E$。
(1)若$∠B= 30^{\circ}$,$∠ACB= 80^{\circ}$,求$∠E$的度数;
(2)试猜想$∠E与∠B$,$∠ACB$之间的数量关系,并证明你的结论。

答案:
(1)解:
∵∠B+∠ACB+∠BAC=180°,∠B=30°,
∠ACB=80°,
∴∠BAC=180°-30°-80°=70°.
∵AD平分∠BAC,
∴∠1=∠2=35°,
∴∠3=∠1+∠B=35°+30°=65°.
∵PE⊥AD,
∴∠3+∠E=90°,
∴∠E=90°-65°=25°.
(2)∠ACB-∠B=2∠E.
证明:
∵∠B+∠ACB+∠BAC=180°,
∴∠BAC=180°-∠B-∠ACB.
∵AD平分∠BAC,
∴∠1=∠2=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠ACB),
∴∠3=∠1+∠B=∠2+∠B=$\frac{1}{2}$(180°-∠B-∠ACB)+∠B=90°$\frac{+1}{2}$∠B$\frac{-1}{2}$∠ACB.
∵PE⊥AD,
∴∠3+∠E=90°,
∴90°$\frac{+1}{2}$∠B$\frac{-1}{2}$∠ACB+∠E=90°,即∠ACB-∠B=2∠E.
10. 在$\triangle ABC$中,$BD平分∠ABC交AC于点D$,$E是线段AC$上的动点(不与点$D$重合),过点$E作EF//BC交射线BD于点F$,$∠CEF的平分线所在直线与射线BD交于点G$。
(1)如图,点$E在线段AD$上运动。
①若$∠ABC= 40^{\circ}$,$∠C= 60^{\circ}$,则$∠BGE$的度数是______
50°
;
②若$∠A= 70^{\circ}$,则$∠BGE$的度数是______
55°
;
③探究$∠BGE与∠A$之间的数量关系,并说明理由。
解:
∵∠ABC+∠C=180°-∠A,EF//BC,
∴∠C=∠DEF,
∴∠ABC+∠DEF=180°-∠A.
∵BD平分∠ABC,EG平分∠CEF,
∴∠CBD=$\frac{1}{2}$∠ABC,∠FEG=$\frac{1}{2}$∠DEF,
∴∠CBD+∠FEG=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠DEF=$\frac{1}{2}$×(180°-∠A)=90°-$\frac{1}{2}$∠A.
∵EF//BC,
∴∠EFG=∠CBD,
∴∠EFG+∠FEG=90°-$\frac{1}{2}$∠A,
∴∠BGE=∠EFG+∠FEG=90°-$\frac{1}{2}$∠A.
(2)若点$E在线段DC$上运动,$∠BGE与∠A$之间的数量关系与(1)③中的数量关系是否相同?若不相同,请直接写出$∠BGE与∠A$之间的数量关系,无需说明理由。
不相同.∠BGE=$\frac{1}{2}$∠A.
答案:
(1)①50° ②55°
③解:
∵∠ABC+∠C=180°-∠A,EF//BC,
∴∠C=∠DEF,
∴∠ABC+∠DEF=180°-∠A.
∵BD平分∠ABC,EG平分∠CEF,
∴∠CBD=$\frac{1}{2}$∠ABC,∠FEG=$\frac{1}{2}$∠DEF,
∴∠CBD+∠FEG=$\frac{1}{2}$∠ABC$\frac{+1}{2}$∠DEF=$\frac{1}{2}$×(180°-∠A)=90°$\frac{-1}{2}$∠A.
∵EF//BC,
∴∠EFG=∠CBD,
∴∠EFG+∠FEG=90°$\frac{-1}{2}$∠A,
∴∠BGE=∠EFG+∠FEG=90°$\frac{-1}{2}$∠A.
(2)解:不相同.∠BGE=$\frac{1}{2}$∠A.