1. 分一分,填一填。
$75^{\circ}$ $148^{\circ}$ $90^{\circ}$ $100^{\circ}$ $65^{\circ}$
$45^{\circ}$ $176^{\circ}$ $180^{\circ}$ $360^{\circ}$ $120^{\circ}$
锐角:(
$75^{\circ}$ $65^{\circ}$ $45^{\circ}$
) 钝角:(
$148^{\circ}$ $100^{\circ}$ $176^{\circ}$ $120^{\circ}$
)
直角:(
$90^{\circ}$
) 平角:(
$180^{\circ}$
)
周角:(
$360^{\circ}$
)
答案:锐角:$75^{\circ}$ $65^{\circ}$ $45^{\circ}$ 钝角:$148^{\circ}$ $100^{\circ}$ $176^{\circ}$ $120^{\circ}$ 直角:$90^{\circ}$ 平角:$180^{\circ}$ 周角:$360^{\circ}$
2. (1) 新情境 真实生活 如图是
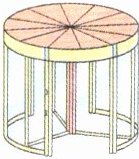
一道三翼式旋转门,由三扇门隔成相等的三部分。每两扇门所形成的夹角是(
120
)$^{\circ}$,是(
钝
)角。
答案:120 钝
解析:
解:因为旋转门是圆形,圆周角为360°,被三扇门隔成相等的三部分,所以每两扇门所形成的夹角是360°÷3=120°。120°大于90°小于180°,是钝角。
120 钝
(2) 军训时,小雨根据口令,向左转一次,转了(
90
)$^{\circ}$;向后转一次,转了(
180
)$^{\circ}$;连续向右转(
12
)次,才能转动$1080^{\circ}$。
答案:90 180 12
解析:
向左转一次,转了$90^{\circ}$;向后转一次,转了$180^{\circ}$;因为每次向右转$90^{\circ}$,所以转动$1080^{\circ}$需要的次数为$1080÷90 = 12$次。
$90$;$180$;$12$
(3) 5时整,钟面上时针与分针所形成的较小角是(
150
)$^{\circ}$。从5时到6时,时针转过(
30
)$^{\circ}$,形成的角是(
锐
)角;分针转过(
360
)$^{\circ}$,形成的角是(
周
)角。
答案:150 30 锐 360 周
解析:
5时整,钟面上时针指向5,分针指向12,中间有5个大格。钟面一圈为360°,共12个大格,每个大格的度数为360°÷12=30°,所以较小角是5×30°=150°。
从5时到6时,时针转过1个大格,转过的度数为30°,30°小于90°,形成的角是锐角;分针转一圈,转过360°,形成的角是周角。
150 30 锐 360 周
3. (2025·徐州铜山区期末)一般在为幼儿园小朋友设计滑梯时,滑梯攀登架与地面的夹角大约是$70^{\circ}$,滑道与地面的夹角大约是$30^{\circ}$。请在下面方框中画出滑梯的示意图,并标出角度。
答案:
4. 图中一共有(
10
)个角,其中锐角有(
4
)个,直角有(
3
)个,钝角有(
2
)个,平角有(
1
)个。
答案:10 4 3 2 1
解析:
图中一共有(10)个角,其中锐角有(4)个,直角有(3)个,钝角有(2)个,平角有(1)个。
5. 如图是由一个长方形和一个正方形拼成的,则$∠1+∠2= $(
90
)$^{\circ}$。

答案:90
解析:
解:设长方形与正方形的公共顶点处,除∠1和∠2外的第三个角为∠3。
因为长方形的四个角为直角,正方形的四个角为直角,
所以∠1 + ∠3 = 90°,∠2 + ∠3 = 90°,
则∠1 = 90° - ∠3,∠2 = 90° - ∠3,
又因为∠1 + ∠2 + ∠3 = 180°(平角定义),
将∠1和∠2代入得:(90° - ∠3) + (90° - ∠3) + ∠3 = 180°,
化简得:180° - ∠3 = 180°,所以∠3 = 0°(此步骤可省略,直接利用∠1 + ∠2 = 180° - ∠3,而∠3 = 90° - ∠1,代入得∠1 + ∠2 = 90°),
故∠1 + ∠2 = 90°。
90
6. 把一张长方形纸的一个角折起来(如图),若$∠2= 130^{\circ}$,则$∠1= $( )$^{\circ}$。

答案:25 解析:如图,折起来的两个角的度数相等,即$∠1=∠3$。又因为$∠2+∠1+∠3=180^{\circ}$,$∠2=130^{\circ}$,所以$∠1=∠3=(180^{\circ}-∠2)÷2=(180^{\circ}-130^{\circ})÷2=25^{\circ}$。

7. 如图,已知$∠1= ∠2= ∠3$,且图中所有锐角的和是$200^{\circ}$,求$∠1$的度数。

答案:$∠1=200^{\circ}÷10=20^{\circ}$ 解析:题图中所有锐角的和是$∠1+∠2+∠3+(∠1+∠2)+(∠2+∠3)+(∠1+∠2+∠3)=200^{\circ}$,且$∠1=∠2=∠3$,所以$200^{\circ}$就是10个$∠1$的度数和,即$∠1=200^{\circ}÷10=20^{\circ}$。
解析:
解:由图可知,所有锐角分别为$∠1$、$∠2$、$∠3$、$∠1+∠2$、$∠2+∠3$、$∠1+∠2+∠3$。
因为$∠1=∠2=∠3$,设$∠1=x$,则所有锐角的和为:
$x + x + x + (x + x) + (x + x) + (x + x + x)$
$=3x + 2x + 2x + 3x$
$=10x$
已知所有锐角的和是$200^{\circ}$,所以$10x=200^{\circ}$,解得$x=20^{\circ}$,即$∠1=20^{\circ}$。
答:$∠1$的度数为$20^{\circ}$。