5. 明明要爷爷出一道趣味题,爷爷给他念了一个顺口溜:
湖边春色分外娇,一株杏树两株桃,
平湖周围三千米,五米一株都栽到,
漫步湖畔美景色,可知桃杏各多少?
你知道桃树和杏树各有多少株吗?
答案:$3000÷5=600$(株) 杏树:$600÷(2+1)=200$(株) 桃树:$600-200=400$(株)
6. 有趣的平行。
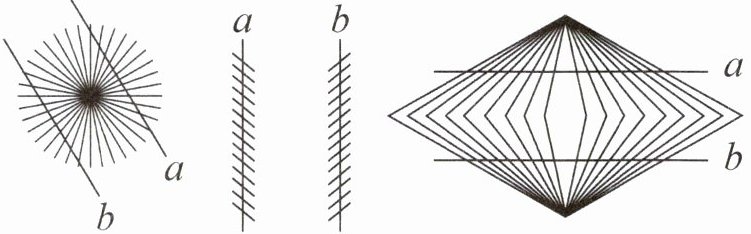
(1)上面各组直线a、b( )互相平行的。(填“是”或“不是”)
(2)利用所学知识,检验上面各组直线a、b是否互相平行。(保留画图痕迹)
上面的现象称为黑林错觉,指两条平行的直线被许多在平行线中间相交的直线分割后,看起来这两条平行线中间部分显得弯曲。
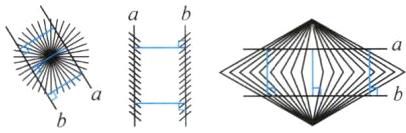
答案:(1) 是 (2) 利用平行线间距离处处相等进行检验,如图。
7. 小刚将两张长方形纸上、下摆放,下面一张纸固定不动,上面一张纸绕点A按图中方向旋转。他发现,在旋转的过程中,$∠1和∠2$的度数在变化,他将相应的度数记录在下表中。

(1)请将上表填写完整。
(从左往右)$75^{\circ }$ $35^{\circ }$ $40^{\circ }$ $80^{\circ }$
(2)比较$∠1和∠2$的度数,我发现:______。
$∠1$和$∠2$的度数和是$90^{\circ }$
(3)当上面的长方形纸按箭头方向旋转到两张长方形纸的短边重合时,$∠1= $( )°,$∠2= $( )°。
90
0
(4)在两张长方形纸的短边重合后,上面的长方形纸继续绕点A按下图中的方向旋转,如果$∠1是130^{\circ }$,那么你知道$∠2$是多少度吗?这时,$∠1和∠2$的度数有什么关系?

$∠2=90^{\circ }-(180^{\circ }-130^{\circ })=40^{\circ }$ $∠1-∠2=90^{\circ }$ $∠2$是$40^{\circ }$,$∠1$和$∠2$的度数差是$90^{\circ }$。
答案:(1) (从左往右)$75^{\circ }$ $35^{\circ }$ $40^{\circ }$ $80^{\circ }$ (2)$∠1$和$∠2$的度数和是$90^{\circ }$ (3) 90 0 (4)$∠2=90^{\circ }-(180^{\circ }-130^{\circ })=40^{\circ }$ $∠1-∠2=90^{\circ }$ $∠2$是$40^{\circ }$,$∠1$和$∠2$的度数差是$90^{\circ }$。
8. (南通如东县期末)“142857”是个非常神奇的数,它的2倍、3倍、4倍、5倍与6倍仍然是用1,4,2,8,5,7这6个数字组成的。比如:$142857×2= 285714,142857×3= 428571$……小亮写了一串的“142857”:142857142857142857……照他这样继续写下去,左起第75个数字是(
2
),前75个数字的和是(
331
)。
答案:2 331
解析:
142857为一个循环周期,周期长度为6。
75÷6=12(组)……3(个),所以第75个数字是周期中的第3个数字,即2。
一个周期数字之和:1+4+2+8+5+7=27。
前75个数字之和:12×27 + (1+4+2)=324+7=331。
左起第75个数字是2,前75个数字的和是331。
2 331