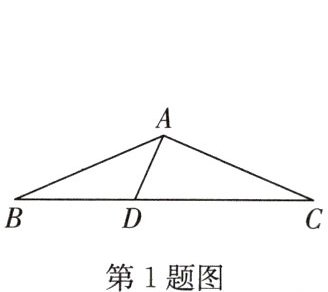
1. (2024·兰州)如图,在$\triangle ABC$中,$AB=AC,∠BAC=130^{\circ },DA⊥AC$,则$∠ADB=$ (
B
)
A.$100^{\circ }$
B.$115^{\circ }$
C.$130^{\circ }$
D.$145^{\circ }$
答案:B
2. 某城市几条道路的位置关系如图所示,道路$AB// CD$,道路$AB$与$AE$的夹角$∠BAE=54^{\circ }$,城市规划部门想新修一条道路$CE$,要求使$CF=EF$,则$∠E$的度数为 (
C
)

A.$23^{\circ }$
B.$25^{\circ }$
C.$27^{\circ }$
D.$30^{\circ }$
答案:C
3. 如图,在$\triangle ABC$中,$BC=5cm$,$BP$,$CP$分别是$∠ABC$和$∠ACB$的平分线,且$PD// AB$,$PE// AC$,则$\triangle PDE$的周长是
5
cm.

答案:5
4. (2024·徐州期末)如图,在$\triangle ABC$中,$AB=AC$,$AD⊥BC$,点$E$在$CA$的延长线上,$EF// AD$.求证:$AE=AF$.

证明:
$\because AB = AC$,$AD \perp BC$,$\therefore \angle BAD = \angle DAC$。$\because EF // AD$,$\therefore \angle BAD = \angle AFE$,$\angle DAC = \angle E$,$\therefore \angle E = \angle AFE$,$\therefore AE = AF$。
答案:证明:$\because AB = AC$,$AD \perp BC$,
$\therefore \angle BAD = \angle DAC$。$\because EF // AD$,
$\therefore \angle BAD = \angle AFE$,$\angle DAC = \angle E$,
$\therefore \angle E = \angle AFE$,$\therefore AE = AF$。
5. 如图,在$\triangle ABC$中,$AD⊥BC$,$∠B=62^{\circ }$,$AB+BD=CD$,则$∠BAC$的度数为 (
A
)

A.$87^{\circ }$
B.$88^{\circ }$
C.$89^{\circ }$
D.$90^{\circ }$
答案:A
6. (2023·如皋月考)如图,在$\triangle ABC$中,$D$为边$AC$上一点,且$BD$平分$∠ABC$,过点$A$作$AE⊥BD$于点$E$.若$∠ABC=52^{\circ }$,$∠C=32^{\circ }$,$AB=5.2$,$BC=9.8$,则$AE=$
2.3
.

答案:1. 首先求$\angle BAC$的度数:
根据三角形内角和定理$\angle BAC+\angle ABC + \angle C=180^{\circ}$。
已知$\angle ABC = 52^{\circ}$,$\angle C = 32^{\circ}$,则$\angle BAC=180^{\circ}-\angle ABC - \angle C=180^{\circ}-52^{\circ}-32^{\circ}=96^{\circ}$。
2. 然后利用角平分线性质:
因为$BD$平分$\angle ABC$,所以$\angle ABD=\angle CBD=\frac{1}{2}\angle ABC$。
又$\angle ABC = 52^{\circ}$,则$\angle ABD = 26^{\circ}$。
3. 接着延长$AE$交$BC$于点$F$:
因为$AE\perp BD$,即$\angle AEB=\angle FEB = 90^{\circ}$。
在$\triangle ABE$和$\triangle FBE$中,$\left\{\begin{array}{l}\angle ABE=\angle FBE\\ BE = BE\\ \angle AEB=\angle FEB\end{array}\right.$。
根据$ASA$(角 - 边 - 角)判定定理,$\triangle ABE\cong\triangle FBE$。
所以$AE = FE$,$AB = FB=5.2$(全等三角形对应边相等)。
那么$FC=BC - FB$,已知$BC = 9.8$,$FB = 5.2$,则$FC=9.8 - 5.2=4.6$。
且$\angle BAE=\angle BFE$(全等三角形对应角相等)。
因为$\angle BAC = 96^{\circ}$,所以$\angle BFE=\angle BAE$,$\angle FAC=\angle BAC-\angle BAE$,$\angle AFC = 180^{\circ}-\angle BFE$,所以$\angle FAC=\angle C$。
所以$AF = FC$(等角对等边)。
又因为$AF = 2AE$,$FC = 4.6$。
所以$AE = 2.3$。
故答案为$2.3$。
7. 如图,$\triangle ABC$的面积为$10cm^{2}$,$AP$垂直于$∠ABC$的平分线$BP$于点$P$,则$\triangle PBC$的面积是
$5cm^{2}$
.

答案:1. 延长$AP$交$BC$于点$Q$:
因为$BP$平分$\angle ABC$,所以$\angle ABP = \angle QBP$。
又因为$BP\perp AP$,即$\angle APB=\angle QPB = 90^{\circ}$,且$BP = BP$(公共边)。
根据$ASA$(角 - 边 - 角)判定定理:在$\triangle ABP$和$\triangle QBP$中,$\left\{\begin{array}{l}\angle ABP=\angle QBP\\BP = BP\\\angle APB=\angle QPB\end{array}\right.$,所以$\triangle ABP\cong\triangle QBP$。
由全等三角形的性质可知$AP = QP$,$S_{\triangle ABP}=S_{\triangle QBP}$(全等三角形面积相等)。
2. 分析$\triangle APC$和$\triangle QPC$的面积关系:
对于$\triangle APC$和$\triangle QPC$,它们有相同的高(以$C$到$AQ$的距离为高),且$AP = QP$(已证)。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),设$C$到$AQ$的距离为$h$,$S_{\triangle APC}=\frac{1}{2}AP\cdot h$,$S_{\triangle QPC}=\frac{1}{2}QP\cdot h$,所以$S_{\triangle APC}=S_{\triangle QPC}$。
3. 计算$S_{\triangle PBC}$:
因为$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle APC}+S_{\triangle PBC}$,又$S_{\triangle ABP}=S_{\triangle QBP}$,$S_{\triangle APC}=S_{\triangle QPC}$。
而$S_{\triangle PBC}=S_{\triangle QBP}+S_{\triangle QPC}$。
所以$S_{\triangle PBC}=\frac{1}{2}S_{\triangle ABC}$。
已知$S_{\triangle ABC}=10cm^{2}$,则$S_{\triangle PBC}=5cm^{2}$。
故答案为$5cm^{2}$。