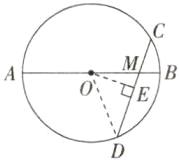
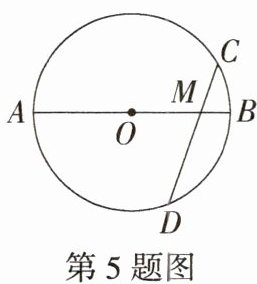
5.「2024江苏扬州高邮期末」如图,$\odot O的直径AB和弦CD相交于点M$,已知$AM= 5$,$BM= 1$,$\angle CMB= 60^{\circ}$,则$CD$的长为______.
答案:答案 $2\sqrt{6}$
解析 如图,连接OD,过点O作OE⊥CD于点E,则CD=2DE。
∵∠CMB=60°,∴∠OME=∠CMB=60°,∵OE⊥CD,∴∠OEM=90°,∴∠MOE=90°−60°=30°,∵AM=5,BM=1,∴OD=OB=$\frac{1}{2}(AM+BM)=3$,∴OM=3−1=2,∴EM=1,∴OE=$\sqrt{OM^{2}-ME^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,∴DE=$\sqrt{OD^{2}-OE^{2}}=\sqrt{3^{2}-(\sqrt{3})^{2}}=\sqrt{6}$,∴CD=2$\sqrt{6}$。
方法总结:在解决有关弦的问题时,常将半径、圆心到弦的垂线段、弦的一半构建在一个直角三角形中,再利用勾股定理解浃问题。