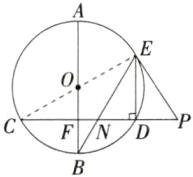
16.如图,$AB为\odot O$的直径,$E是弧AD$上一点,弦$DE// AB$,且$DE\perp弦CD$,连接$BE交CD于点N$,点$P在CD$的延长线上,$PN= PE$.若$OF= 6$,$BF= 4$,求$PN$的长.
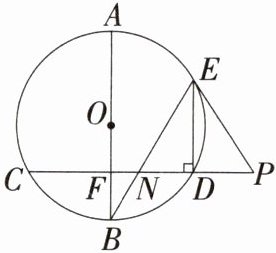
答案:解析 如图,连接CE,∵DE⊥CD,∴∠CDE=90°,∴CE为⊙O的直径,∴CE经过点O。
∵PN=PE,∴∠PEN=∠PNE,
∵OB=OE,∴∠OEB=∠OBE,由DE//AB,DE⊥CD 可得AB⊥CD,∴∠OBE+∠BNF=90°,∴∠OEB+∠PEN=90°,即∠PEC=90°,
∵AB⊥CD,∴CF=DF,
∵OC=OE,∴OF为△CED的中位线,∴DE=2OF=12,由OF=6,BF=4得OC=OB=10,∴CE=20,
∴CD=$\sqrt{CE^{2}-DE^{2}}=16$,设PD=x,则PC=x+16。
在Rt△PDE和Rt△PCE中,由勾股定理,得PD²+DE²=PE²=PC²-CE²,即x²+12²=(x+16)²-20²,解得x=9,∴PD=9。
∴PE=$\sqrt{PD^{2}+DE^{2}}=15$,∴PN=PE=15。