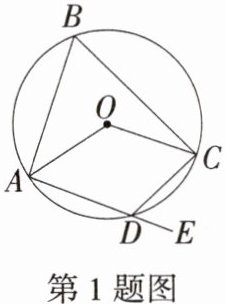
1.「2024四川广元中考」如图,已知四边形ABCD是$\odot O$的内接四边形,E为AD延长线上一点,$∠AOC= 128^{\circ }$,则$∠CDE$等于(
A
)
A.$64^{\circ }$
B.$60^{\circ }$
C.$54^{\circ }$
D.$52^{\circ }$
答案:A $\because \angle AOC = 128^{\circ}$,$\therefore \angle ABC = 64^{\circ}$,$\because$ 四边形 $ABCD$ 是 $\odot O$ 的内接四边形,$\therefore \angle ADC = 180^{\circ} - 64^{\circ} = 116^{\circ}$,$\therefore \angle CDE = 180^{\circ} - \angle ADC = 64^{\circ}$。故选 A。
可推出圆内接四边形的外角等于内对角
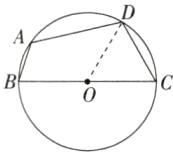
2.「2023江苏淮安中考」如图,四边形ABCD是$\odot O$的内接四边形,BC是$\odot O$的直径,$BC= 2CD$,则$∠BAD$的度数是______$^{\circ }$。

答案:答案 120
解析 如图,连接 $OD$,$\because BC$ 是 $\odot O$ 的直径,$BC = 2CD$,$\therefore OC = OD = CD$,$\therefore \triangle COD$ 为等边三角形,$\therefore \angle C = 60^{\circ}$。$\because$ 四边形 $ABCD$ 是 $\odot O$ 的内接四边形,$\therefore \angle BAD + \angle C = 180^{\circ}$,$\therefore \angle BAD = 120^{\circ}$。
3.「2024江苏南京鼓楼二模」如图,四边形ABCD是$\odot O$的内接四边形,BE是$\odot O$的直径,连接CE,若$∠BAD= 105^{\circ }$,则$∠DCE= $
15
$^{\circ }$。

答案:答案 15
解析 $\because$ 四边形 $ABCD$ 是 $\odot O$ 的内接四边形,$\therefore \angle BAD + \angle DCB = 180^{\circ}$,$\because \angle BAD = 105^{\circ}$,$\therefore \angle DCB = 180^{\circ} - 105^{\circ} = 75^{\circ}$。$\because BE$ 是 $\odot O$ 的直径,$\therefore \angle BCE = 90^{\circ}$,$\therefore \angle DCE = 90^{\circ} - 75^{\circ} = 15^{\circ}$。
4.「2025重庆渝北月考」如图,在$\odot O$的内接四边形ABCD中,$AB= AD$,$∠E= 130^{\circ }$,则$∠C$的度数为______$^{\circ }$。

答案:答案 100
解析 如图,连接 $BD$,$\because$ 四边形 $ABDE$ 是圆内接四边形,$\therefore \angle E + \angle ABD = 180^{\circ}$。$\because \angle E = 130^{\circ}$,$\therefore \angle ABD = 180^{\circ} - 130^{\circ} = 50^{\circ}$。$\because AB = AD$,$\therefore \angle ADB = \angle ABD = 50^{\circ}$,$\therefore \angle BAD = 180^{\circ} - 2 \times 50^{\circ} = 80^{\circ}$。$\because$ 四边形 $ABCD$ 是圆内接四边形,$\therefore \angle C = 180^{\circ} - 80^{\circ} = 100^{\circ}$。

5.「2025江苏南京建邺月考」如图,点A,B,C,D,E在$\odot O$上,且$∠B+∠D= 155^{\circ }$,则$\overset{\frown }{AE}$所对的圆心角为______$^{\circ }$。

答案:答案 50
解析 如图,连接 $BA$,$OA$,$OE$,$\because$ 点 $A$,$B$,$C$,$D$,$E$ 在 $\odot O$ 上,$\therefore$ 四边形 $ABCD$ 是圆内接四边形,$\therefore \angle ABC + \angle D = 180^{\circ}$。$\because \angle EBC + \angle D = 155^{\circ}$,$\therefore \angle ABC - \angle CBE = 25^{\circ}$,即 $\angle ABE = 25^{\circ}$。$\because \angle AOE = 2 \angle ABE$,$\therefore \angle AOE = 50^{\circ}$,即 $\overset{\frown}{AE}$ 所对的圆心角为 $50^{\circ}$。

6.「2025浙江温州期中,★☆」如图,四边形ABCD内接于$\odot O$,$AE⊥CB$交CB的延长线于点E,若BA平分$∠DBE$,$AD= 6$,$CE= 4$,则AE的长为( )

A.2
B.3
C.$2\sqrt {3}$
D.$2\sqrt {5}$
答案:D 如图,连接 $AC$,$\because$ 四边形 $ABCD$ 内接于 $\odot O$,$\therefore \angle ADC + \angle ABC = 180^{\circ}$。$\because \angle ABE + \angle ABC = 180^{\circ}$,$\therefore \angle ABE = \angle ADC$。$\because \overset{\frown}{AD} = \overset{\frown}{AD}$,$\therefore \angle ABD = \angle ACD$,$\because BA$ 平分 $\angle DBE$,$\therefore \angle ABE = \angle ABD$,$\therefore \angle ADC = \angle ACD$,$\therefore AC = AD$,$\because AD = 6$,$\therefore AC = 6$,$\therefore$ 在 $Rt \triangle AEC$ 中,由勾股定理得 $AE = \sqrt{AC^{2} - CE^{2}} = 2\sqrt{5}$。故选 D。

7.「2024河北石家庄赵县期末,★☆」如图,$\odot C$过原点O,且与两坐标轴分别交于点A、B,点A的坐标为$(0,5)$,点M是第三象限内$\overset{\frown }{OB}$上一点,$∠BMO= 120^{\circ }$,则$\odot C$的半径为(
B
)

A.4
B.5
C.6
D.$2\sqrt {3}$
答案:B $\because$ 四边形 $ABMO$ 是圆内接四边形,$\therefore \angle BAO + \angle BMO = 180^{\circ}$。$\because \angle BMO = 120^{\circ}$,$\therefore \angle BAO = 60^{\circ}$。$\because AB$ 是圆的直径,$\therefore \angle AOB = 90^{\circ}$,$\therefore \angle ABO = 90^{\circ} - \angle BAO = 30^{\circ}$,$\therefore AO = \frac{1}{2}AB$。$\because$ 点 $A$ 的坐标是 $(0, 5)$,$\therefore OA = 5$,$\therefore AB = 10$,$\therefore \odot C$ 的半径为 5。故选 B。
8.学科 「2024北京丰台期末,★☆」如图,点O为线段AB的中点,$∠ACB= ∠ADB= 90^{\circ }$,连接OC、OD、CD,则下面结论不一定成立的是(
D
)

A.$OC= OD$
B.$∠BDC= ∠BAC$
C.$∠BCD+∠BAD= 180^{\circ }$
D.AC平分$∠BAD$
答案:D $\because$ 点 $O$ 为线段 $AB$ 的中点,$\angle ACB = \angle ADB = 90^{\circ}$,$\therefore OD = \frac{1}{2}AB$,$OC = \frac{1}{2}AB$,$\therefore OD = OC = OA = OB$,$\therefore$ 点 $A$、$D$、$C$、$B$ 在以 $O$ 为圆心,$OA$ 长为半径的圆上,故 A 选项不符合题意;由圆周角定理可得 $\angle BDC = \angle BAC$,故 B 选项不符合题意;$\because$ 四边形 $ABCD$ 是圆内接四边形,$\therefore \angle BCD + \angle BAD = 180^{\circ}$,故 C 选项不符合题意;$\because$ 在 $\odot O$ 中,$\overset{\frown}{CD}$ 和 $\overset{\frown}{BC}$ 不一定相等,$\therefore \angle DAC$ 和 $\angle BAC$ 不一定相等,$\therefore AC$ 不一定平分 $\angle BAD$,故 D 选项符合题意。故选 D。
9.新 「2024山东临沂蒙阴期末」如图,A,P,B,C是$\odot O$上的四点,$∠APC= ∠CPB= 60^{\circ }$,过点C作$CM// BP$交PA的延长线于点M,下列结论正确的是______
①②③④
(填序号)。

答案:答案 ①②③④
解析 $\because A$,$P$,$B$,$C$ 是 $\odot O$ 上的四点,$\therefore$ 四边形 $APBC$ 是圆内接四边形,$\therefore \angle PBC + \angle PAC = 180^{\circ}$,$\because \angle PAC + \angle MAC = 180^{\circ}$,$\therefore \angle MAC = \angle PBC$,故①正确;$\because \angle APC = \angle CPB = 60^{\circ}$,$\therefore \angle ABC = \angle APC = 60^{\circ}$,$\angle BAC = \angle BPC = 60^{\circ}$,$\therefore \angle ABC = \angle BAC = 60^{\circ}$,$\therefore \triangle ABC$ 是等边三角形,故②正确;$\because$ 四边形 $APBC$ 是 $\odot O$ 的内接四边形,$\therefore \angle MAC = \angle PBC$,$\angle ACB + \angle APB = 180^{\circ}$,$\because CM // BP$,$\therefore \angle M + \angle APB = 180^{\circ}$,$\therefore \angle M = \angle ACB$,$\because \triangle ABC$ 是等边三角形,$\therefore \angle ACB = \angle BAC = 60^{\circ}$,$AC = BC$,$\because \angle BPC = \angle BAC = 60^{\circ}$,$\therefore \angle M = \angle BPC$,在 $\triangle ACM$ 与 $\triangle BCP$ 中,$\begin{cases} \angle M = \angle BPC, \\ \angle MAC = \angle PBC, \\ AC = BC, \end{cases}$ $\therefore \triangle ACM \cong \triangle BCP (AAS)$。$\therefore PB = AM$,$\therefore PA + PB = PA + AM = PM$,$\because \angle M = \angle BPC = 60^{\circ}$,$\angle APC = 60^{\circ}$,$\therefore \triangle MPC$ 为等边三角形,$\therefore PC = PM$,$\therefore PC = PA + PB$,故③④正确。故答案为①②③④。