答案：答案 ①②③④
解析 在 Rt△ABC 中, AB = AC, 点 D 为 BC 的中点, ∴∠C = ∠BAD = 45°, AD = BD = CD, ∠ADC = 90°, ∴∠ADF + ∠CDF = 90°, ∵∠MDN = 90°, ∴∠ADE + ∠ADF = 90°, ∴∠ADE = ∠CDF, 在△AED 与△CFD 中, $\begin{cases}∠EAD = ∠C, \\ AD = CD, \\ ∠ADE = ∠CDF,\end{cases}$ ∴△AED ≌ △CFD(ASA), ∴AE = CF, ED = FD, 故②正确. 又∵∠EDF = 90°, ∴△DEF 为等腰直角三角形, 故①正确. ∵AE = CF, AB = AC, ∴AB - AE = AC - CF, ∴BE = AF, 在△BDE 和△ADF 中, $\begin{cases}BE = AF, \\ DE = DF, \\ BD = AD,\end{cases}$ ∴△BDE ≌ △ADF(SSS), 故③正确. ∵△AED ≌ △CFD, △BDE ≌ △ADF, ∴S_{△AED} = S_{△CFD}, S_{△BDE} = S_{△ADF}, ∴S_{四边形 AEDF} = S_{△AED} + S_{△ADF} = $\frac{1}{2}$S_{△ABC}, 故④正确. 综上所述, 正确结论是①②③④.

答案：
解析 (1) 如图①所示(答案不唯一).
(2) 如图②所示.
(3) 如图③所示.

答案：
解析 (1) 如图, △A₁B₁C₁ 即为所求.
(2) 如图, △A₂B₂C₂ 即为所求.
(3) 如图, 旋转中心的坐标为(-4, 0).

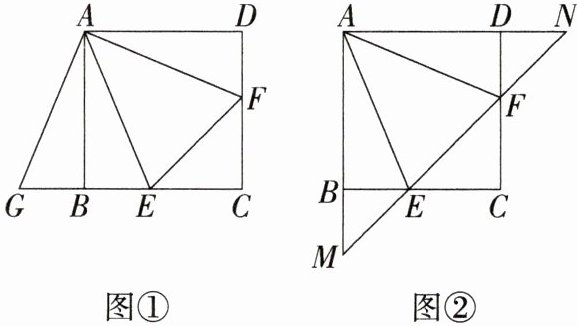
答案：
证明 (1) ∵△ADF 绕着点 A 顺时针旋转 90°, 得到△ABG, ∴AG = AF, BG = DF, ∠GAF = 90°, G、B、E 三点共线. ∵∠EAF = 45°, ∴∠GAE = ∠GAF - ∠EAF = 45°, ∴∠GAE = ∠EAF, 在△AEG 和△AEF 中, $\begin{cases}AG = AF, \\ ∠GAE = ∠FAE, \\ AE = AE,\end{cases}$ ∴△AEG ≌ △AEF(SAS), ∴GE = EF. ∵GE = BE + GB = BE + DF, ∴BE + DF = EF.
(2) 将△ADF 绕点 A 顺时针旋转 90°, 得到△ABG, 连接 GM, 如图所示.

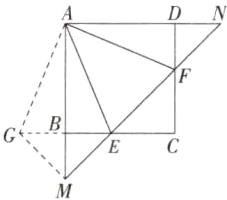
∵四边形 ABCD 是正方形, ∴AB = BC = CD = AD, ∠ADC = ∠ABC = ∠C = 90°. ∵∠CEF = 45°, ∴△CEF 为等腰直角三角形, CE = CF, 易知△DFN 与△BEM 也是等腰直角三角形, ∴DF = DN, BM = BE. ∵BC = CD, ∴BE = DF. 由(1)知 BG = DF, ∴BG = DF = DN = BE = BM, ∴△BGM 也是等腰直角三角形, ∠BMG = 45°, ∵∠EMB = 45°, ∴∠EMG = 90°, ∴EG² = MG² + ME², 易知 MG = $\sqrt{2}$BM, NF = $\sqrt{2}$DF, ∴MG = NF, ∴EG² = NF² + ME². 由(1)知 EG = EF, ∴EF² = ME² + NF².