1.「2024 山东潍坊中考」下列著名曲线中,既是轴对称图形也是中心对称图形的是 (
C
)
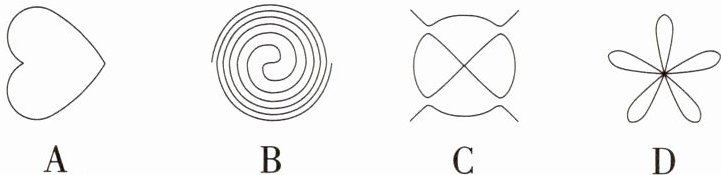
答案:C A. 是轴对称图形, 但不是中心对称图形, 不符合题意; B. 不是轴对称图形, 是中心对称图形, 不符合题意; C. 既是轴对称图形, 又是中心对称图形, 符合题意; D. 是轴对称图形, 但不是中心对称图形, 不符合题意. 故选 C.
2.「2025 云南昭通水富期中」如图,$△DEC是由△ABC$绕点 C 顺时针旋转得到的,$∠B= 25^{\circ },∠1= 65^{\circ }$,则旋转角的度数是 (
A
)

A.$90^{\circ }$
B.$85^{\circ }$
C.$65^{\circ }$
D.$25^{\circ }$
答案:A ∵△DEC 是由△ABC 绕点 C 顺时针旋转得到的, ∴旋转角的度数等于∠BCE 的度数, ∵∠B = 25°, ∠1 = 65°, ∴∠BCE = 180° - ∠1 - ∠B = 90°. 故选 A.
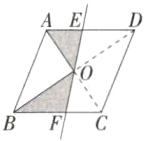
3.「2024 陕西咸阳秦都模拟」如图,点 O 是菱形 ABCD 的对称中心,连接 OA、OB,$OA= 4,OB= 6$,EF 为过点 O 的一条直线,点 E、F 分别在边 AD、BC 上,则图中阴影部分的面积为 ( )

A.24
B.16
C.18
D.12
答案:D 如图, 连接 OC、OD, ∵点 O 是菱形 ABCD 的对称中心, ∴A、O、C 三点共线, B、O、D 三点共线, O 是 AC 与 BD 的交点, 且 AC⊥BD, ∴CO = AO = 4, DO = BO = 6, ∵EF 为过点 O 的一条直线, ∴△AOE 与△COF 关于点 O 对称, ∴S_{阴影部分} = S_{△BOC} = $\frac{1}{2}$×6×4 = 12. 故选 D.
4.「2025 山东德州宁津期中」若点$P(-m,3-m)$关于原点的对称点在第四象限,则 m 满足 (
B
)
A.$m>3$
B.$0<m<3$
C.$m<0$
D.$m<0或m>3$
答案:B ∵点 P(-m, 3 - m)关于原点的对称点为(m, m - 3), 且点(m, m - 3)在第四象限, ∴$\begin{cases}m > 0, \\ m - 3 < 0,\end{cases}$ ∴0 < m < 3. 故选 B.
5.如图,若正方形 EFGH 是由正方形 ABCD 绕某点旋转得到的,则旋转中心可以是 (
A
)

A.点 M 或点 O 或点 N
B.点 E 或点 O 或点 C
C.点 E 或点 O 或点 N
D.点 M 或点 O 或点 C
答案:A 若以点 M 为旋转中心, 把正方形 ABCD 顺时针旋转 90°, 则 A 点的对应点为 H, B 点的对应点为 E, C 点的对应点为 F, D 点的对应点为 G, 则可得到正方形 EFGH; 若以点 O 为旋转中心, 把正方形 ABCD 旋转 180°, 则 A 点的对应点为 G, B 点的对应点为 H, C 点的对应点为 E, D 点的对应点为 F, 则可得到正方形 EFGH; 若以点 N 为旋转中心, 把正方形 ABCD 逆时针旋转 90°, 则 A 点的对应点为 F, B 点的对应点为 G, C 点的对应点为 H, D 点的对应点为 E, 则可得到正方形 EFGH. 故选 A.
6.「2024 四川广元中考」如图,将$△ABC$绕点 A 顺时针旋转$90^{\circ }得到△ADE$,点 B,C 的对应点分别为点 D,E,连接 CE,点 D 恰好落在线段 CE 上,若$CD= 3,BC= 1$,则 AD 的长为 ( )

A.$\sqrt {5}$
B.$\sqrt {10}$
C.2
D.$2\sqrt {2}$
答案:A 如图, 连接 BD, ∵将△ABC 绕点 A 顺时针旋转 90°得到△ADE, ∴AB = AD, AC = AE, ∠BAD = ∠CAE = 90°, ∠ACB = ∠E, ∴△ABD 和△ACE 均为等腰直角三角形. ∴∠ACB = ∠E = ∠ACE = 45°, ∴∠BCD = ∠ACB + ∠ACE = 90°. ∵CD = 3, BC = 1, ∴BD = $\sqrt{CD^{2} + BC^{2}} = \sqrt{3^{2} + 1^{2}} = \sqrt{10}$, ∴AD = $\frac{\sqrt{2}}{2}$BD = $\frac{\sqrt{2}}{2}$×$\sqrt{10}$ = $\sqrt{5}$. 故选 A.

7.「2025 广西南宁期中」如图,$△OAB$中,$∠AOB= 60^{\circ },OA= 6$,点 B 的坐标为$(8,0)$,将$△OAB$绕点 A 逆时针旋转得到$△CAD$,当点 O 的对应点 C 落在 OB 上时,点 D 的坐标为 ( )

A.$(10,4\sqrt {3})$
B.$(10,4)$
C.$(5\sqrt {3},5)$
D.$(5\sqrt {3},4\sqrt {3})$
答案:A 由旋转的性质可知, ∠ACD = ∠AOB = 60°, AC = AO = 6, CD = OB = 8, ∴△AOC 是等边三角形, ∴OC = OA = 6, ∠ACO = 60°, ∴∠DCB = 180° - ∠ACO - ∠ACD = 60°. 如图, 过点 D 作 DE⊥x 轴, 垂足为 E, ∴∠DEC = 90°, ∴∠CDE = 180° - ∠DCB - ∠DEC = 30°, ∴CE = $\frac{1}{2}$CD = 4, ∴OE = OC + CE = 10, 在 Rt△DCE 中, DE = $\sqrt{CD^{2} - CE^{2}}$ = 4$\sqrt{3}$, ∴点 D 的坐标为(10, 4$\sqrt{3}$). 故选 A.

8.「2024 黑龙江大庆中考」如图,在矩形 ABCD 中,$AB= 10,BC= 6$,点 M 是 AB 边的中点,点 N 是 AD 边上任意一点,将线段 MN 绕点 M 顺时针旋转$90^{\circ }$,点 N 旋转到点$N'$,连接$BN'$,则$△MBN'$周长的最小值为 ( )

A.15
B.$5+5\sqrt {5}$
C.$10+5\sqrt {2}$
D.18
答案:B 如图, 过点 N'作 EF//AB, 交 AD、BC 于 E、F, 过点 M 作 MG⊥EF 于点 G, ∵四边形 ABCD 是矩形, ∴AB//CD, ∴AB//EF//CD, ∴四边形 AMGE 和 BMGF 都是矩形, ∴∠A = ∠MGN' = 90°, 由旋转的性质得∠NMN' = 90°, MN = MN', ∴∠AMN = 90° - ∠NMG = ∠GMN', ∴△AMN ≌ △GMN'(AAS), ∴MG = AM, ∵AB = 10, M 为 AB 的中点, ∴AM = BM = MG = 5, ∴点 N'在平行于 AB, 且与 AB 的距离为 5 的直线上运动, 作点 M 关于直线 EF 的对称点 M', 连接 M'B 交直线 EF 于点 N', 此时△MBN'的周长取得最小值, 最小值 = BM + BM', ∵BM = 5, MM' = 5 + 5 = 10, ∴BM + BM' = 5 + $\sqrt{5^{2} + 10^{2}}$ = 5 + 5$\sqrt{5}$. 故选 B.

9.「2024 吉林长春二道月考」如图,阴影部分组成的图案既是关于 x 轴成轴对称的图形,又是关于坐标原点 O 成中心对称的图形.若点 A 的坐标为$(1,3)$,点 B 的坐标为$(3,1)$,点 M 的坐标为$(a,b)$,点 N 的坐标为$(c,d)$,则$a+c$的值为____
-2
.

答案:答案 -2
解析 由题图可知, 点 A 和点 N 关于 x 轴对称, 点 M 和点 B 关于坐标原点 O 成中心对称, 因为点 A 的坐标为(1, 3), 点 B 的坐标为(3, 1), 所以 a = -3, c = 1, 所以 a + c = -3 + 1 = -2.