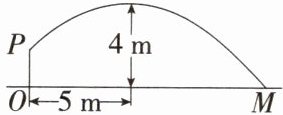
10.「2024广西中考」如图,壮壮同学投掷实心球,出手点(点P处)的高度OP是$\frac {7}{4}m$,出手后实心球沿一段抛物线运行,到达最高点时,与出手点的水平距离是5m,距地面的高度是4m.若实心球落地点为M,则$OM= $____m.
答案:答案 $ \frac{35}{3} $
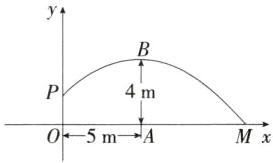
解析 如图,以 $ O $ 为坐标原点,$ OM $ 所在直线为 $ x $ 轴,$ OP $ 所在直线为 $ y $ 轴,建立直角坐标系,由题意可知 $ P \left( 0, \frac{7}{4} \right) $,$ B(5, 4) $,其中点 $ B $ 为抛物线的顶点. 设抛物线的顶点式为 $ y = a(x - 5)^{2} + 4(a \neq 0) $,将 $ P \left( 0, \frac{7}{4} \right) $ 代入上式,解得 $ a = - \frac{9}{100} $,即抛物线的解析式为 $ y = - \frac{9}{100}(x - 5)^{2} + 4 $,$ \because M $ 为抛物线与 $ x $ 轴的交点,令 $ y = - \frac{9}{100}(x - 5)^{2} + 4 = 0 $,解得 $ x_{1} = \frac{35}{3} $,$ x_{2} = - \frac{5}{3} $(舍),$ \therefore OM = \frac{35}{3} \text{m} $.
11.「2024福建中考」(12分)如图,已知二次函数$y= x^{2}+bx+c$的图象与x轴交于A,B两点,与y轴交于点C,其中$A(-2,0),C(0,-2)$.
(1)求二次函数的表达式.
$y = x^{2} + x - 2$
(2)若P是二次函数图象上的一点,且点P在第二象限,线段PC交x轴于点D,$\triangle PDB的面积是\triangle CDB$面积的2倍,求点P的坐标.
$(-3, 4)$

答案:解析
(1) 将 $ A(-2, 0) $,$ C(0, -2) $ 代入 $ y = x^{2} + bx + c $,得 $ \begin{cases} 4 - 2b + c = 0, \\ c = -2, \end{cases} $ 解得 $ \begin{cases} b = 1, \\ c = -2, \end{cases} $ $ \therefore $ 二次函数的表达式为 $ y = x^{2} + x - 2 $.
(2) 设 $ P(m, n)(m < 0, n > 0) $,则 $ n = m^{2} + m - 2 $,$ \because C(0, -2) $,$ \therefore CO = 2 $. $ \because \triangle PDB $ 的面积是 $ \triangle CDB $ 面积的 2 倍,$ \therefore \frac{1}{2}BD \cdot n = 2 \times \frac{1}{2}BD \cdot CO $,$ \therefore n = 2CO = 4 $,则 $ m^{2} + m - 2 = 4 $,$ \therefore m_{1} = -3 $,$ m_{2} = 2 $(舍去),$ \therefore $ 点 $ P $ 的坐标为 $ (-3, 4) $.
12.「2024北京中考」(12分)在平面直角坐标系xOy中,已知抛物线$y= ax^{2}-2a^{2}x(a≠0)$.
(1)当$a= 1$时,求抛物线的顶点坐标.
(2)已知$M(x_{1},y_{1})和N(x_{2},y_{2})$是抛物线上的两点,若对于$x_{1}= 3a,3≤x_{2}≤4$,都有$y_{1}<y_{2}$,求a的取值范围.
答案:解析
(1) 把 $ a = 1 $ 代入 $ y = ax^{2} - 2a^{2}x $,得 $ y = x^{2} - 2x = (x - 1)^{2} - 1 $,$ \therefore $ 抛物线的顶点坐标为 $ (1, -1) $.
(2) $ \because - \frac{-2a^{2}}{2a} = a $,$ \therefore $ 抛物线的对称轴为直线 $ x = a $,分两种情况讨论:
① 当 $ a > 0 $ 时,如图,由 $ y_{1} < y_{2} $ 可得 $ 3a < 3 $,$ \therefore a < 1 $,$ \therefore 0 < a < 1 $;

② 当 $ a < 0 $ 时,如图,由 $ y_{1} < y_{2} $ 可得 $ 4 < -a $,解得 $ a < -4 $.

综上,$ 0 < a < 1 $ 或 $ a < -4 $.
13.「2024山东烟台中考」(16分)每年5月的第三个星期日为全国助残日,2024年的主题是“科技助残,共享美好生活”.某公司新研发了一批便携式轮椅计划在该月销售.根据市场调查,每辆轮椅盈利200元时,每天可售出60辆;单价每降低10元,每天可多售出4辆.公司决定在成本不变的情况下降价销售,但每辆轮椅的利润不低于180元.设每辆轮椅降价x元,每天的销售利润为y元.
(1)求y与x的函数关系式.每辆轮椅降价多少元时,每天的销售利润最大?最大利润为多少元?
(2)全国助残日当天,该公司共获得销售利润12160元,请问这天售出了多少辆轮椅?
答案:解析
(1) $ y = (200 - x) \left( 60 + 4 \times \frac{x}{10} \right) = -0.4x^{2} + 20x + 12000 = -0.4(x - 25)^{2} + 12250 $,$ \therefore $ 函数图象的对称轴为直线 $ x = 25 $,当 $ x < 25 $ 时,$ y $ 随 $ x $ 的增大而增大. $ \because 200 - x \geq 180 $,$ \therefore x \leq 20 $,$ \therefore $ 当 $ x = 20 $ 时,销售利润最大,最大利润为 $ -0.4 \times (20 - 25)^{2} + 12250 = 12240 $(元).
答:$ y $ 与 $ x $ 的函数关系式为 $ y = -0.4x^{2} + 20x + 12000 $;每辆轮椅降价 20 元时,每天的销售利润最大,为 12240 元.
(2) 由题意得 $ 12160 = -0.4(x - 25)^{2} + 12250 $,则 $ 0.4(x - 25)^{2} = 90 $,$ \therefore (x - 25)^{2} = 225 $. 解得 $ x_{1} = 40 $(不合题意,舍去),$ x_{2} = 10 $. $ \therefore $ 售出轮椅的辆数为 $ 60 + 4 \times \frac{10}{10} = 64 $.
答:这天售出了 64 辆轮椅.