1.「2025吉林四平期末」已知抛物线$y= -(x-3)^{2}+\frac {1}{4}$,下列说法正确的是 (
C
)
A.开口向上
B.对称轴是直线$x= -3$
C.顶点坐标为$(3,\frac {1}{4})$
D.当$x<-3$时,y随x的增大而减小
答案:C A. $a = -1 < 0$,图象开口向下,原说法错误,不符合题意;B. 对称轴是直线 $x = 3$,原说法错误,不符合题意;C. 顶点坐标为 $ \left( 3, \frac{1}{4} \right) $,原说法正确,符合题意;D. 当 $x < -3$ 时, $y$ 随 $x$ 的增大而增大,原说法错误,不符合题意. 故选 C.
2.「2024内蒙古包头中考」将抛物线$y= x^{2}+2x$向下平移2个单位后,所得新抛物线的顶点式为 (
A
)
A.$y= (x+1)^{2}-3$
B.$y= (x+1)^{2}-2$
C.$y= (x-1)^{2}-3$
D.$y= (x-1)^{2}-2$
答案:A $y = x^{2} + 2x = (x + 1)^{2} - 1$,将抛物线 $y = x^{2} + 2x$ 向下平移 2 个单位,得抛物线 $y = (x + 1)^{2} - 1 - 2$,$ \therefore $ 所得新抛物线的顶点式为 $y = (x + 1)^{2} - 3$. 故选 A.
3.「2024浙江宁波鄞州期中」抛物线$y= 2x^{2}-4x+1$与坐标轴的交点的个数是 (
B
)
A.4
B.3
C.2
D.1
答案:B $ \because a = 2$,$b = -4$,$c = 1$,$ \therefore b^{2} - 4ac = (-4)^{2} - 4 \times 2 \times 1 = 8 > 0$,$ \therefore $ 抛物线 $y = 2x^{2} - 4x + 1$ 与 $x$ 轴有 2 个交点. $ \because x = 0$ 时,$y = 1$,$ \therefore $ 抛物线与 $y$ 轴有 1 个交点,$ \therefore $ 该抛物线与坐标轴有 3 个交点. 故选 B.
易错点:容易把坐标轴错看成 $x$ 轴,从而漏掉与 $y$ 轴的交点.
4.「2025黑龙江哈尔滨香坊期中」在同一平面直角坐标系中,二次函数$y= ax^{2}+bx+c与一次函数y= ax+c$的大致图象可能是(
C
)
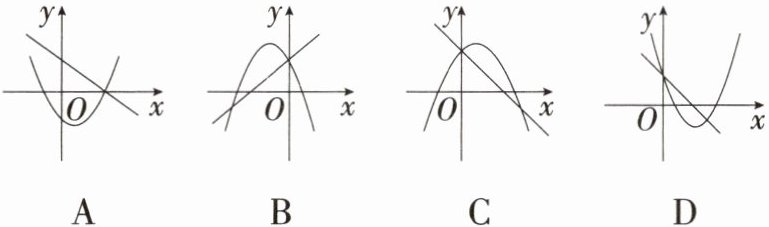
答案:C 由题意得,一次函数和二次函数的图象都经过 $y$ 轴上的点 $ (0, c) $,$ \therefore $ 两个函数图象交于 $y$ 轴上的同一点,排除 A;当 $a > 0$ 时,二次函数图象开口向上,直线经过第一、三象限,排除 D;当 $a < 0$ 时,二次函数图象开口向下,直线经过第二、四象限,排除 B. 故选 C.
5.「2024四川广安中考」如图,二次函数$y= ax^{2}+bx+c$(a,b,c为常数,$a≠0$)的图象与x轴交于点

$A(-\frac {3}{2},0)$,对称轴是直线$x= -\frac {1}{2}$,有以下结论:①$abc<0$;②若点$(-1,y_{1})和点(2,y_{2})$都在抛物线上,则$y_{1}<y_{2}$;③$am^{2}+bm≤\frac {1}{4}a-\frac {1}{2}b$(m为任意实数);④$3a+4c= 0$.其中正确的有 (
B
)
A.1个
B.2个
C.3个
D.4个
答案:B $ \because $ 二次函数图象开口向下,与 $y$ 轴交于正半轴,$ \therefore a < 0$,$c > 0$,$ \because - \frac{b}{2a} = - \frac{1}{2} < 0$,$ \therefore b < 0$,$ \therefore abc > 0$,故①错误;$ \because $ 对称轴是直线 $x = - \frac{1}{2} $,且 $ \left| -1 - \left( - \frac{1}{2} \right) \right| < \left| 2 - \left( - \frac{1}{2} \right) \right| $,$ \therefore y_{1} > y_{2} $,故②错误;$ \because $ 当 $x = m$ 时,$y = am^{2} + bm + c$,当 $x = - \frac{1}{2}$ 时,函数取得最大值,为 $ \frac{1}{4}a - \frac{1}{2}b + c $,$ \therefore $ 对于任意实数 $m$,有 $am^{2} + bm + c \leq \frac{1}{4}a - \frac{1}{2}b + c $,$ \therefore am^{2} + bm \leq \frac{1}{4}a - \frac{1}{2}b $,故③正确;$ \because - \frac{b}{2a} = - \frac{1}{2} $,$ \therefore b = a $,$ \because $ 当 $x = - \frac{3}{2}$ 时,$y = 0$,$ \therefore \frac{9}{4}a - \frac{3}{2}b + c = 0 $,$ \therefore 9a - 6b + 4c = 0 $,即 $ 3a + 4c = 0 $,故④正确. 故选 B.
6.如图1,在$\triangle ABC$中,$AB= 10,BC= 6,AC= 8$,点P为线段AB上的动点,以每秒1个单位长度的速度从点A向点B移动,到达点B时停止.过点P作$PM⊥AC$于点M,作$PN⊥BC$于点N,连接MN,线段MN的长度y与点P的运动时间t(秒)的函数关系如图2所示,则函数图象最低点E的坐标为 ( )


A.$(5,5)$
B.$(6,\frac {24}{5})$
C.$(\frac {32}{5},\frac {24}{5})$
D.$(\frac {32}{5},5)$
答案:C 如图,过点 $C$ 作 $CD \perp AB$ 于 $D$,连接 $CP$,$ \because $ 在 $ \triangle ABC $ 中,$AB = 10$,$BC = 6$,$AC = 8$,$ \therefore AC^{2} + BC^{2} = 8^{2} + 6^{2} = 100 = 10^{2} = AB^{2} $,$ \therefore \triangle ABC $ 是直角三角形,$ \angle ACB = 90^{\circ} $,$ \therefore S_{\triangle ABC} = \frac{1}{2}AC \cdot BC = \frac{1}{2}AB \cdot CD $,$ \therefore CD = \frac{AC \cdot BC}{AB} = \frac{24}{5} $,$ \therefore AD = \sqrt{AC^{2} - CD^{2}} = \frac{32}{5} $. $ \because PM \perp AC $,$PN \perp BC $,$ \angle ACB = 90^{\circ} $,$ \therefore $ 四边形 $CMPN$ 是矩形,$ \therefore MN = CP $,当点 $P$ 与点 $D$ 重合时,$CP$ 的值最小,此时 $MN$ 取最小值,为 $ \frac{24}{5} $,$AP = AD = \frac{32}{5} $,$ \therefore $ 点 $E$ 的坐标为 $ \left( \frac{32}{5}, \frac{24}{5} \right) $. 故选 C.

7.「2025江苏苏州工业园区期中」若$y= (m-1)x^{|m|}+1$是关于x的二次函数,且该函数图象开口向下,则$m=$
$-2$
.
答案:答案 $-2$
解析 由题意得 $ |m| = 2 $,且 $ m - 1 < 0 $,解得 $ m = -2 $.
8.「2024吉林长春中考」若抛物线$y= x^{2}-x+c$(c是常数)与x轴没有交点,则c的取值范围是
$c > \frac{1}{4}$
.
答案:答案 $ c > \frac{1}{4} $
解析 由题意,得 $ \Delta = (-1)^{2} - 4c < 0 $,$ \therefore c > \frac{1}{4} $.
9.「2024河南新乡长垣期末」二次函数$y= ax^{2}+bx+c$的部分对应值列表如下:

则一元二次方程$ax^{2}+bx+c= -7$的解为
$x_{1} = 0$,$x_{2} = 2$
.
答案:答案 $ x_{1} = 0 $,$ x_{2} = 2 $
解析 由题表可得,二次函数 $ y = ax^{2} + bx + c $ 图象的对称轴为直线 $ x = \frac{-3 + 5}{2} = 1 $,当 $ x = 0 $ 时,$ y = -7 $,$ \therefore $ 当 $ x = 2 $ 时,$ y = -7 $,$ \therefore $ 一元二次方程 $ ax^{2} + bx + c = -7 $ 的解为 $ x_{1} = 0 $,$ x_{2} = 2 $.