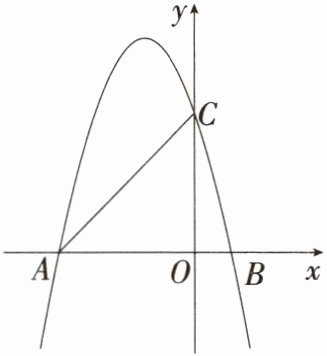
4.「2025湖北宜昌西陵期中」如图,已知二次函数$y= -x^2+bx+c$的图象与x轴交于点A(-4,0)和点B,与y轴交于点C(0,4),连接AC.点P为x轴上方抛物线上一动点(点P不与点A,C重合),设点P的横坐标为t.
(1)求该二次函数的解析式.
(2)连接PC,当∠PCA= 45°时,求t的值.
(3)设以A,O,C,P为顶点的四边形的面积为S.
①求S关于t的函数解析式.
②根据S的不同取值,试探索点P的个数情况.
答案:解析 (1)∵ 二次函数$y=-x^{2}+bx+c$的图象与x轴交于点A(-4,0),与y轴交于点C(0,4),∴ $\begin{cases}-16-4b+c=0,\\c=4,\end{cases}$解得$\begin{cases}b=-3,\\c=4,\end{cases}$∴ 该二次函数的解析式为$y=-x^{2}-3x+4$.
(2)由题意得$P(t,-t^{2}-3t+4)$,∵ A(-4,0),C(0,4),∴ OA=OC=4, ∴ ∠OAC=∠OCA=45°.∵ ∠PCA=45°,∴ ∠PCO=90°,∴ PC⊥OC,∵ OA⊥OC,∴ PC//OA.
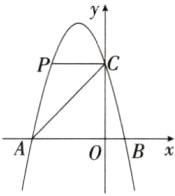
∴ 点P的纵坐标为4,∴ $-t^{2}-3t+4=4$,解得t=0或t=-3,∵ t≠0,∴ t=-3.
(3)①令y=0,则$-x^{2}-3x+4=0$,解得x=-4或x=1,∵ 点B在x轴正半轴上,∴ B(1,0),∴ OB=1.当点P在AC的上方,即-4<t<0时,过点P作PD⊥OA于点D,

则$PD=-t^{2}-3t+4$,$OD=0-t=-t$,∴ AD=t-(-4)=t+4,∴ $S=S_{△PAD}+S_{梯形PDOC}=\frac{1}{2}AD·PD+\frac{1}{2}(PD+OC)·OD=\frac{1}{2}(t+4)(-t^{2}-3t+4)+\frac{1}{2}(-t^{2}-3t+4+4)×(-t)=-2t^{2}-8t+8$.当点P在AC的下方,即0<t<1时,过点P作PE⊥OC于点E,

则PE=t,∴ $S=S_{△OAC}+S_{△OPC}=\frac{1}{2}OA·OC+\frac{1}{2}OC·PE=\frac{1}{2}×4×4+\frac{1}{2}×4t=2t+8$.
综上,$S=\begin{cases}-2t^{2}-8t+8(-4<t<0),\\2t+8(0<t<1).\end{cases}$
②当-4<t<0时,$S=-2t^{2}-8t+8=-2(t+2)^{2}+16$,∵ -2<0,∴ 当t=-2时,S有最大值,为16,∵ |-4-(-2)|=|0-(-2)|,∴ 当t=-4或t=0时,$-2(t+2)^{2}+16=8$,∴ 8<S≤16.当0<t<1时,S=2t+8,∴ 8<S<10.
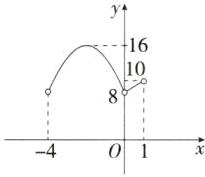
函数$S=\begin{cases}-2t^{2}-8t+8(-4<t<0),\\2t+8(0<t<1)\end{cases}$的大致图象如图所示,由图象可知,当8<S<10时,存在3个符合条件的点P;当10≤S<16时,存在2个符合条件的点P;当S=16时,存在1个符合条件的点P.