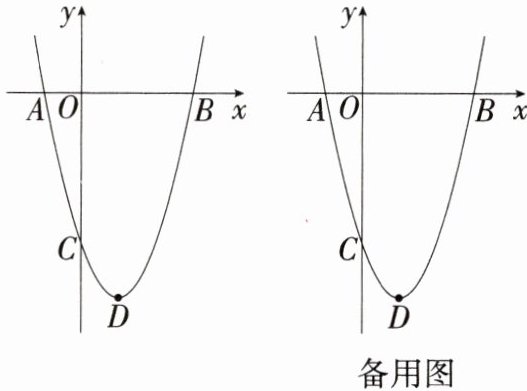
2. [2024四川宜宾中考改编]如图,抛物线$y= x^2+bx+c$与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-4),其顶点为D.
(1)求抛物线的表达式及顶点D的坐标.
(2)在y轴上是否存在一点M,使得△BDM的周长最小?若存在,求出点M的坐标;若不存在,请说明理由.
(3)抛物线对称轴上是否存在一动点F,使得|BF-CF|的值最大?若存在,求出点F的坐标;若不存在,请说明理由.
答案:解析 (1)把A(−1,0),C(0,−4)代入y=x²+bx+c得{c = -4,1 - b + c = 0,}解得{b = -3,c = -4,}
∴抛物线的表达式为y=x²−3x−4.
∵y=x²−3x−4=(x - $\frac{3}{2}$)² - $\frac{25}{4}$,∴抛物线顶点D的坐标为($\frac{3}{2}$,-$\frac{25}{4}$).
(2)在y轴上存在一点M,使得△BDM的周长最小.
在y=x²−3x−4中,令y=0,得0=x²−3x−4,
解得x=4或x=−1,∴B(4,0),
如图,连接BD,易知BD=$\sqrt{(4 - \frac{3}{2})² + (-\frac{25}{4})²}$=$\frac{5\sqrt{29}}{4}$,
∴若使△BDM的周长最小,只需使DM+BM的值最小.
作D($\frac{3}{2}$,-$\frac{25}{4}$)关于y轴的对称点D'(-$\frac{3}{2}$,-$\frac{25}{4}$),

连接BD'交y轴于M,连接DM,
则DM=D'M,∴DM+BM=D'M+BM=BD',
此时DM+BM的值最小,最小值为线段BD'的长,此时△BDM的周长也最小.
由B(4,0),D'(-$\frac{3}{2}$,-$\frac{25}{4}$)得直线BD'的解析式为y=$\frac{25}{22}$x - $\frac{50}{11}$,令x=0得y=-$\frac{50}{11}$,
∴点M的坐标为(0,-$\frac{50}{11}$).
(3)存在.
∵点B关于图象对称轴的对称点为A(−1,0),∴|BF−CF|=|AF−CF|≤AC,
∴当A,C,F三点共线时,|BF−CF|有最大值,为AC的长.
连接AC并延长交抛物线对称轴于点F(图略),则点F即为所求,
由A(−1,0),C(0,−4)得,直线AC的表达式为y=−4x−4,当x=$\frac{3}{2}$时,y=−10,
故点F($\frac{3}{2}$,-10).