5.「2024天津中考,★☆」从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的函数关系式是$h= 30t-5t^{2}(0≤t≤6)$.有下列结论:
①小球从抛出到落地需要6s;
②小球运动中的高度可以是30m;
③小球运动2s时的高度小于运动5s时的高度.
其中,正确结论的个数是(
C
)
A.0
B.1
C.2
D.3
答案:C ①令 $ h = 0 $,则 $ 30t - 5t^2 = 0 $,解得 $ t_1 = 0 $,$ t_2 = 6 $,$ \therefore $ 小球从抛出到落地需要 $ 6s $,故①正确;② $ h = 30t - 5t^2 = -5(t^2 - 6t) = -5(t - 3)^2 + 45 $,$ \because -5 < 0 $,$ \therefore $ 当 $ t = 3 $ 时,$ h $ 有最大值,最大值为 $ 45 $,$ \therefore $ 小球运动中的高度可以是 $ 30m $,故②正确;③ $ t = 2 $ 时,$ h = 30 \times 2 - 5 \times 4 = 40 $,$ t = 5 $ 时,$ h = 30 \times 5 - 5 \times 25 = 25 $,$ \therefore $ 小球运动 $ 2s $ 时的高度大于运动 $ 5s $ 时的高度,故③错误。故选 C。
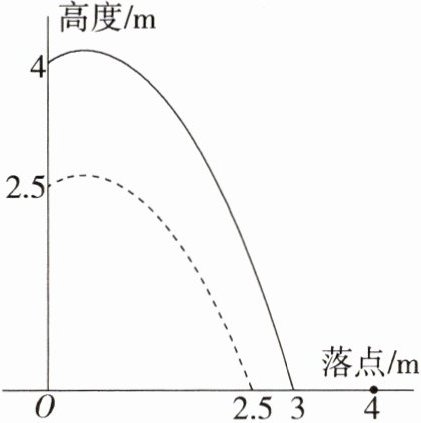
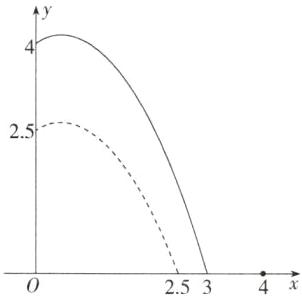
6.「2022四川南充中考,★☆」如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高2.5m时,水柱落点距O点2.5m,喷头高4m时,水柱落点距O点3m,那么喷头高______m时,水柱落点距O点4m.
答案:答案 8
解析 如图,以 $ O $ 为原点建立平面直角坐标系,由题意可知,在调整喷头高度的过程中,水柱的形状不发生变化,当喷头高 $ 2.5m $ 时,设抛物线的解析式为 $ y = ax^2 + bx + 2.5 $,将 $ (2.5, 0) $ 代入解析式得出 $ 6.25a + 2.5b + 2.5 = 0 $,整理得 $ 2.5a + b + 1 = 0 $ ①,当喷头高 $ 4m $ 时,设抛物线的解析式为 $ y = ax^2 + bx + 4 $,将 $ (3, 0) $ 代入解析式得 $ 9a + 3b + 4 = 0 $ ②,联立①②可求出 $ a = -\frac{2}{3} $,$ b = \frac{2}{3} $,设喷头高为 $ h m $ 时,水柱落点距 $ O $ 点 $ 4m $,$ \therefore $ 此时抛物线的解析式为 $ y = -\frac{2}{3}x^2 + \frac{2}{3}x + h $,将 $ (4, 0) $ 代入解析式可得 $ -\frac{2}{3} \times 4^2 + \frac{2}{3} \times 4 + h = 0 $,解得 $ h = 8 $。$ \therefore $ 当喷头高 $ 8m $ 时,水柱落点距 $ O $ 点 $ 4m $。
7.「2024甘肃兰州中考,★☆」在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2,建立平面直角坐标系,水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面OA的竖直高度y(m)与离发射点O的水平距离x(m)的几组对应数据如表:

(1)根据表格,求抛物线的表达式.
解:抛物线的表达式为
$ y = -\frac{1}{25}(x - 15)^2 + 9 $
.
(2)请计算当水火箭飞行至离发射点O的水平距离为5m时,水火箭距离地面的竖直高度.
解:水火箭距离地面的竖直高度为
5
m.

答案:解析 (1) 由题表可得,抛物线的对称轴是直线 $ x = \frac{10 + 20}{2} = 15 $,$ \therefore $ 抛物线的顶点坐标为 $ (15, 9) $。$ \therefore $ 可设抛物线的表达式为 $ y = a(x - 15)^2 + 9 $。又 $ \because $ 抛物线过点 $ (10, 8) $,$ \therefore 25a + 9 = 8 $,$ \therefore a = -\frac{1}{25} $。$ \therefore $ 抛物线的表达式为 $ y = -\frac{1}{25}(x - 15)^2 + 9 $。
(2) 由 (1) 得 $ y = -\frac{1}{25}(x - 15)^2 + 9 $,令 $ x = 5 $,则 $ y = -\frac{1}{25} \times (5 - 15)^2 + 9 = 5 $。$ \therefore $ 当 $ x = 5 $ 时,水火箭距离地面的竖直高度为 $ 5m $。
8.新 课标 模型观念「2025浙江杭州萧山月考」如图,同学们在操场上玩跳大绳游戏,绳甩到最高处时的形状是抛物线,摇绳的两名同学拿绳的手的间距为6米,到地面的距离AO与BD均为1.1米,当绳子甩到最高点C处时,最高点距地面的垂直距离为2.0米.身高为1.6米的小吉站在距点O水平距离为m米处,若他能够正常跳大绳(绳子甩到最高时超过他的头顶),则m的取值范围是______.

答案:答案 $ 1 < m < 5 $
解析 如图,建立平面直角坐标系,由题意可知 $ OD = 6 $,$ A(0, 1.1) $,$ B(6, 1.1) $,最高点 $ C $ 的纵坐标为 $ 2 $,$ \therefore $ 点 $ C $ 的横坐标为 $ \frac{0 + 6}{2} = 3 $,$ \therefore C(3, 2) $,设抛物线的解析式为 $ y = a(x - 3)^2 + 2 $,把 $ A(0, 1.1) $ 代入解析式可得 $ a = -0.1 $,$ \therefore y = -0.1(x - 3)^2 + 2 $,当 $ y = 1.6 $ 时,$ -0.1(x - 3)^2 + 2 = 1.6 $,解得 $ x_1 = 1 $,$ x_2 = 5 $,$ \therefore m $ 的取值范围是 $ 1 < m < 5 $。
