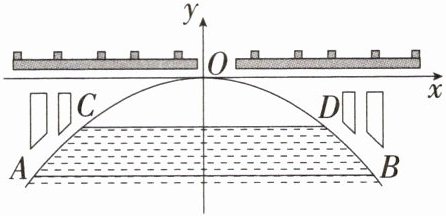
1.「2025安徽宣城月考」下图是根据某拱桥形状建立的平面直角坐标系,从中得到函数$y= -\frac {1}{25}x^{2}$,在正常水位时水面宽$AB= 30m$,当水位上升5m时,水面宽CD为(
D
)
A.8m
B.10m
C.15m
D.20m
答案:D 函数 $ y = -\frac{1}{25}x^2 $ 的图象的对称轴为 $ y $ 轴,$ \because AB = 30 $,$ \therefore $ 点 $ A $ 的横坐标为 $ -15 $,当 $ x = -15 $ 时,$ y = -\frac{1}{25} × (-15)^2 = -9 $,$ \therefore A(-15, -9) $,$ \therefore $ 点 $ C $ 的纵坐标为 $ -9 + 5 = -4 $。当 $ y = -\frac{1}{25}x^2 = -4 $ 时,$ x = -10 $ 或 $ x = 10 $,$ \therefore C(-10, -4) $,$ D(10, -4) $,$ \therefore CD = 10 - (-10) = 20(m) $。故选 D。
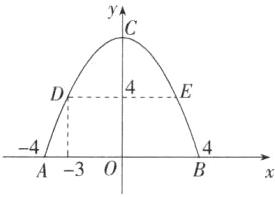
2.「2024吉林长春农安期末」如图,有一个横截面边缘为抛物线形的隧道入口,隧道入口处的底面宽度为8m,两侧距底面4m处各有一盏灯,两灯间的水平距离为6m,则这个隧道入口的最大高度为______m(精确到0.1m).

答案:答案 9.1
解析 建立如图所示的平面直角坐标系。由题意可知 $ A(-4, 0) $,$ B(4, 0) $,$ D(-3, 4) $。设抛物线的解析式为 $ y = ax^2 + c(a \neq 0) $,把 $ (4, 0) $,$ (-3, 4) $ 代入,得 $ \begin{cases} 16a + c = 0, \\ 9a + c = 4, \end{cases} $ 解得 $ \begin{cases} a = -\frac{4}{7}, \\ c = \frac{64}{7}, \end{cases} $ $ \therefore $ 该抛物线的解析式为 $ y = -\frac{4}{7}x^2 + \frac{64}{7} $,则 $ C(0, \frac{64}{7}) $,$ \therefore $ 这个隧道入口的最大高度为 $ \frac{64}{7}m \approx 9.1m $。
3.「2025湖北荆州江陵期中」随着自动化设备的普及,家庭庭院也引入自动喷灌系统.该系统中的喷灌器从喷水口喷出的水柱成抛物线形.下图是喷灌器OA喷水时的示意图,喷水口A点离地高度为0.25m,喷出的水柱在离喷水口水平距离为2m处达到最高点,最高点离地高度为0.45m,且水柱刚好落在庭院围墙和地面的交界点B处,则喷灌器OA与围墙的水平距离OB为( )

A.4m
B.4.5m
C.5m
D.5.5m
答案:C 以 $ O $ 为原点建立坐标系,如图所示,设该抛物线的解析式为 $ y = a(x - 2)^2 + 0.45(a \neq 0) $,$ \because $ 点 $ (0, 0.25) $ 在该函数图象上,$ \therefore 0.25 = a(0 - 2)^2 + 0.45 $,解得 $ a = -\frac{1}{20} $,即 $ y = -\frac{1}{20}(x - 2)^2 + 0.45 $,当 $ y = 0 $ 时,$ 0 = -\frac{1}{20}(x - 2)^2 + 0.45 $,解得 $ x_1 = 5 $,$ x_2 = -1 $(不符合题意,舍去),$ \therefore OB = 5m $。故选 C。

4.「2024吉林长春南关期末」小红看到一处喷水景观,喷出的水柱呈抛物线形,她对此展开研究:测得喷水头P距地面1m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.5m.建立如图所示的平面直角坐标系,并设抛物线的表达式为$y= a(x-h)^{2}+k(a≠0)$,其中x(m)是水柱距喷水头P的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的表达式.
答:抛物线的表达式为$y=$
$-\frac{1}{10}x^2 + x + 1$
.
(2)小红站在水柱正下方且距喷水头P的水平距离为4m,身高1.9m的哥哥在水柱下方走动,当哥哥的头顶恰好接触到水柱时,求小红与哥哥的水平距离.
答:当哥哥的头顶恰好接触到水柱时,小红与哥哥的水平距离是
$3m$或$5m$
.
答案:解析 (1) 由题意知,抛物线的顶点坐标为 $ (5, 3.5) $,则抛物线的表达式可表示为 $ y = a(x - 5)^2 + 3.5(a \neq 0) $,将 $ (0, 1) $ 代入得 $ 1 = 25a + 3.5 $,解得 $ a = -\frac{1}{10} $,$ \therefore y = -\frac{1}{10}(x - 5)^2 + 3.5 = -\frac{1}{10}x^2 + x + 1 $。
答:抛物线的表达式为 $ y = -\frac{1}{10}x^2 + x + 1 $。
(2) 当 $ y = 1.9 $ 时,$ -\frac{1}{10}x^2 + x + 1 = 1.9 $,解得 $ x = 1 $ 或 $ x = 9 $,$ \therefore $ 她与哥哥的水平距离为 $ 4 - 1 = 3(m) $ 或 $ 9 - 4 = 5(m) $。
答:当哥哥的头顶恰好接触到水柱时,小红与哥哥的水平距离是 $ 3m $ 或 $ 5m $。