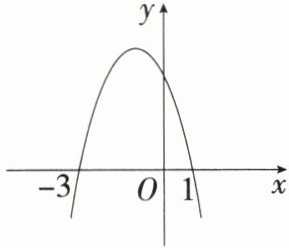
9.「2024山东东营中考,★☆」已知抛物线$y = ax^{2}+bx + c(a \neq 0)$的图象如图所示,则下列结论正确的是(
D
)
A. $abc < 0$
B. $a - b = 0$
C. $3a - c = 0$
D. $am^{2}+bm \leq a - b$($m$为任意实数)
答案:D 由函数图象可知,$a\lt0$,$b\lt0$,$c\gt0$,$\therefore abc\gt0$,故A不符合题意;$\because$ 抛物线与$x$轴的交点坐标为$(-3,0)$和$(1,0)$,$\therefore$ 抛物线的对称轴为直线$x=-\frac{b}{2a}=\frac{-3 + 1}{2}=-1$,$\therefore b = 2a$,$\therefore 2a - b = 0$,故B不符合题意;把$(1,0)$代入解析式,得$a + b + c = 0$,将$b = 2a$代入$a + b + c = 0$,得$a + 2a + c = 0$,$\therefore 3a + c = 0$,故C不符合题意;$\because$ 抛物线的对称轴为直线$x=-1$,且抛物线开口向下,$\therefore$ 当$x=-1$时,函数取得最大值,为$a - b + c$,$\therefore$ 对于抛物线上的任意一点(横坐标为$m$),总有$am^{2}+bm + c\leqslant a - b + c$,$\therefore am^{2}+bm\leqslant a - b$,故D符合题意.故选D.
10.「2025江苏苏州平江中学月考,★☆」二次函数$y = ax^{2}+6x + a$的最小值是8,则$a = $
9
。
答案:答案 9
解析 $\because$ 二次函数$y = ax^{2}+6x + a$的最小值是8,$\therefore a\gt0$,$y_{最小值}=\frac{4a^{2}-36}{4a}=8$,整理,得$a^{2}-8a - 9 = 0$,解得$a = 9$或$-1$,$\because a\gt0$,$\therefore a = 9$.
11.「2024四川成都中考,★☆」在平面直角坐标系$xOy$中,$A(x_{1},y_{1})$,$B(x_{2},y_{2})$,$C(x_{3},y_{3})$是二次函数$y = -x^{2}+4x - 1$图象上的三点。若$0 < x_{1} < 1$,$x_{2} > 4$,则$y_{1}$____
>
____$y_{2}$(填“>”或“<”);若对于$m < x_{1} < m + 1$,$m + 1 < x_{2} < m + 2$,$m + 2 < x_{3} < m + 3$,存在$y_{1} < y_{3} < y_{2}$,则$m$的取值范围是____
$-\frac{1}{2}\lt m\lt1$
____。
答案:答案 $\gt$;$-\frac{1}{2}\lt m\lt1$
解析 $\because y=-x^{2}+4x - 1=-(x - 2)^{2}+3$,$\therefore$ 图象的对称轴为直线$x = 2$,开口向下,$\because 0\lt x_{1}\lt1$,$x_{2}\gt4$,$\therefore 2 - x_{1}\lt x_{2}-2$,即$A(x_{1},y_{1})$比$B(x_{2},y_{2})$离对称轴的距离近,$\therefore y_{1}\gt y_{2}$;$\because m\lt x_{1}\lt m + 1$,$m + 1\lt x_{2}\lt m + 2$,$m + 2\lt x_{3}\lt m + 3$,$\therefore x_{1}\lt x_{2}\lt x_{3}$,$\because$ 对于$m\lt x_{1}\lt m + 1$,$m + 1\lt x_{2}\lt m + 2$,$m + 2\lt x_{3}\lt m + 3$,存在$y_{1}\lt y_{3}\lt y_{2}$,$\therefore x_{1}\lt2$,$x_{3}\gt2$,且$A(x_{1},y_{1})$离对称轴的距离最远,$B(x_{2},y_{2})$离对称轴的距离最近,$\therefore 2 - x_{1}\gt x_{3}-2\gt|x_{2}-2|$,$\therefore x_{1}+x_{3}\lt4$,且$x_{2}+x_{3}\gt4$,$\because 2m + 2\lt x_{1}+x_{3}\lt2m + 4$,$2m + 3\lt x_{2}+x_{3}\lt2m + 5$,$\therefore 2m + 2\lt4$,且$2m + 5\gt4$,解得$-\frac{1}{2}\lt m\lt1$.
12.「2025浙江杭州上城期中,★☆」已知某二次函数图象上部分点的横坐标$x与纵坐标y$的对应值如表所示:

(1) 直接写出$m$,$n$的值,并求当$x$在什么范围时,$y随x$的增大而增大。$m=$
0
,$n=$
4
;当$x$
$\lt2$
时,$y随x$的增大而增大。
(2) 若点$(p,q)$在该二次函数图象上,当$-1 \leq p \leq 4$时,求$q$的取值范围。
$-8\leqslant q\leqslant1$
答案:解析 (1)由表格知$x=-1$时,$y=-8$;$x = 5$时,$y=-8$,$\therefore$ 抛物线的对称轴为直线$x=\frac{-1 + 5}{2}=2$,$\because \frac{1 + 3}{2}=2$,$\therefore$ 点$(1,m)$与点$(3,0)$是关于直线$x = 2$对称的点,$\therefore m = 0$,$\because$ 当$x = 0$时,$y=-3$;当$x = n$时,$y=-3$,$\therefore \frac{0 + n}{2}=2$,$\therefore n = 4$.
结合题表可得,当$x\lt2$时,$y$随$x$的增大而增大.
(2)$\because$ 抛物线对称轴为直线$x = 2$,当$x\lt2$时,$y$随$x$的增大而增大,$\therefore$ 该抛物线开口向下,当$x = 2$时,$y$取得最大值,为1,$\because |-1 - 2|\gt|4 - 2|$,$\therefore$ 当$x=-1$时,$y$取得最小值,为$-8$,$\because -1\leqslant p\leqslant4$,$\therefore -8\leqslant q\leqslant1$.
13. 设$P(x,y_{1})$,$Q(x,y_{2})分别是函数C_{1}$,$C_{2}$图象上的点,当$a \leq x \leq b$时,$-1 \leq y_{1}-y_{2} \leq 1$恒成立,则称函数$C_{1}$,$C_{2}在a \leq x \leq b$上是“逼近函数”,$a \leq x \leq b$为“逼近区间”。则下列结论:①函数$y_{1} = x - 5$,$y_{2} = 3x + 2在1 \leq x \leq 2$上是“逼近函数”;②函数$y_{1} = x - 5$,$y_{2} = x^{2}-4x在3 \leq x \leq 4$上是“逼近函数”;③$0 \leq x \leq 1是函数y_{1} = x^{2}-1$,$y_{2} = 2x^{2}-x$的“逼近区间”;④$2 \leq x \leq 3是函数y_{1} = x - 5$,$y_{2} = x^{2}-4x$的“逼近区间”。其中正确的为(
②③
)
A. ②③
B. ①④
C. ①③
D. ②④
答案:A ①$y_{1}-y_{2}=-2x - 7$,在$1\leqslant x\leqslant2$上,当$x = 1$时,$y_{1}-y_{2}=-9$,当$x = 2$时,$y_{1}-y_{2}=-11$,可知$-11\leqslant y_{1}-y_{2}\leqslant-9$,故函数$y_{1}=x - 5$,$y_{2}=3x + 2$在$1\leqslant x\leqslant2$上不是“逼近函数”,①结论不正确;②$y_{1}-y_{2}=-x^{2}+5x - 5$,在$3\leqslant x\leqslant4$上,当$x = 3$时,$y_{1}-y_{2}=1$,当$x = 4$时,$y_{1}-y_{2}=-1$,所以$-1\leqslant y_{1}-y_{2}\leqslant1$,故函数$y_{1}=x - 5$,$y_{2}=x^{2}-4x$在$3\leqslant x\leqslant4$上是“逼近函数”,②结论正确;③$y_{1}-y_{2}=-x^{2}+x - 1$,在$0\leqslant x\leqslant1$上,当$x=\frac{1}{2}$时,$y_{1}-y_{2}=-\frac{3}{4}$,当$x = 0$或1时,$y_{1}-y_{2}=-1$,可知$-1\leqslant y_{1}-y_{2}\leqslant-\frac{3}{4}$,所以$-1\leqslant y_{1}-y_{2}\leqslant1$成立,故$0\leqslant x\leqslant1$是函数$y_{1}=x^{2}-1$,$y_{2}=2x^{2}-x$的“逼近区间”,③结论正确;④$y_{1}-y_{2}=-x^{2}+5x - 5$,在$2\leqslant x\leqslant3$上,当$x=\frac{5}{2}$时,$y_{1}-y_{2}=\frac{5}{4}$,当$x = 2$或3时,$y_{1}-y_{2}=1$,可知$1\leqslant y_{1}-y_{2}\leqslant\frac{5}{4}$,故$2\leqslant x\leqslant3$不是函数$y_{1}=x - 5$,$y_{2}=x^{2}-4x$的“逼近区间”,④结论不正确.故选A.
例题 「2025浙江宁波慈溪期中」若二次函数$y = x^{2}+2x - 3(m \leq x \leq 2)的最小值为-4$,最大值为5,则$m$的取值范围是____。
答案:答案 $-4\leqslant m\leqslant-1$
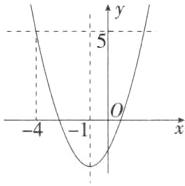
解析 如图,$\because y=x^{2}+2x - 3=(x + 1)^{2}-4$,$\therefore$ 对称轴为直线$x=-1$,函数的最小值为$-4$,$\because m\leqslant x\leqslant2$时,函数的最小值为$-4$,最大值为5,$\therefore$ 令$y = 5$,则$(x + 1)^{2}-4 = 5$,解得$x_{1}=-4$,$x_{2}=2$,$\therefore m$的取值范围为$-4\leqslant m\leqslant-1$.
变式1【定轴动区间】「2025江苏苏州振华中学月考」已知$y = x^{2}-4x + 3$,当$m \leq x \leq m + 2$时,函数$y的最小值为\frac{5}{4}$,则$m$的值为
$-\frac{3}{2}$或$\frac{7}{2}$
。
答案:答案 $-\frac{3}{2}$或$\frac{7}{2}$
解析 $\because$ 二次函数$y=x^{2}-4x + 3=(x - 2)^{2}-1$,$\therefore$ 对称轴为直线$x = 2$.
①若$m + 2\lt2$,即$m\lt0$,则当$x = m + 2$时,$y$的最小值是$\frac{5}{4}$,$\therefore (m + 2 - 2)^{2}-1=m^{2}-1=\frac{5}{4}$,$\therefore m=-\frac{3}{2}$或$m=\frac{3}{2}$(舍去);
②若$m\gt2$,则当$x = m$时,$y$的最小值为$\frac{5}{4}$,$\therefore (m - 2)^{2}-1=\frac{5}{4}$,$\therefore m=\frac{7}{2}$或$m=\frac{1}{2}$(舍去);
③若$m\lt2\lt m + 2$,则当$x = 2$时,$y$的最小值为$-1$,不符合题意.
综上所述,$m$的值为$-\frac{3}{2}$或$\frac{7}{2}$.
变式2【动轴定区间】当$1 \leq x \leq 4$时,函数$y = x^{2}-2ax - 1有最小值-5$,则实数$a$的值是
2
。
答案:答案 2
解析 易知函数$y=x^{2}-2ax - 1$的图象开口向上,对称轴为直线$x=-\frac{-2a}{2\times1}=a$,
若$a\leqslant1$,则当$x = 1$时,函数取最小值,
此时$y = 1-2a - 1=-5$,解得$a = 2.5$(不合题意,舍去);
若$a\geqslant4$,则当$x = 4$时,函数取最小值,
此时$y = 16-8a - 1=-5$,解得$a = 2.5$(不合题意,舍去);
若$1\lt a\lt4$,则当$x = a$时,函数取最小值,
此时$y=a^{2}-2a^{2}-1=-5$,解得$a_{1}=2$,$a_{2}=-2$(舍去).
综上,实数$a$的值是2.