1.「2025重庆南川期中」关于抛物线$y = -x^{2}+2x - 3$的判断,下列说法正确的是(
D
)
A. 抛物线的开口方向向上
B. 抛物线的对称轴是直线$x = -1$
C. 当$x < 1$时,$y随x$的增大而减小
D. 抛物线与$y轴的交点坐标为(0,-3)$
答案:D $\because$ 抛物线$y=-\frac{x^{2}}{2}+2x - 3=-\frac{1}{2}(x - 1)^{2}-\frac{5}{2}$,$\therefore$ 该抛物线的开口向下,抛物线的对称轴是直线$x = 1$,当$x\lt1$时,$y$随$x$的增大而增大,故选项A、B、C说法错误,不符合题意;$\because$ 当$x = 0$时,$y=-3$,$\therefore$ 抛物线与$y$轴的交点坐标为$(0,-3)$,故选项D正确,符合题意.故选D.
2.「2025浙江湖州南浔期中」已知二次函数$y = ax^{2}+bx + c$,其中$a < 0$,$b < 0$,$c > 0$,则该二次函数图象大致是(
B
)
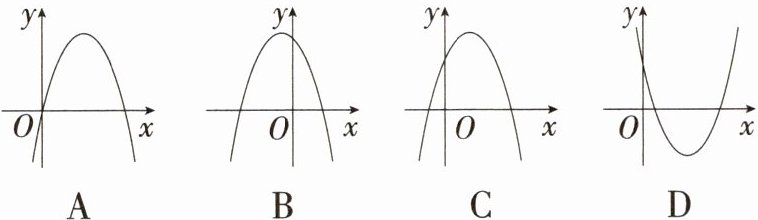
答案:B $\because$ 二次函数$y = ax^{2}+bx + c$,$a\lt0$,$b\lt0$,$c\gt0$,$\therefore$ 该函数图象开口向下,对称轴在$y$轴的左侧,与$y$轴交于正半轴,只有B选项中的图象符合.故选B.
方法解读 抛物线的“左同右异”
对于二次函数$y = ax^{2}+bx + c(a\neq0)$,图象对称轴为直线$x=-\frac{b}{2a}$,易得当$a$,$b$同号时,$x=-\frac{b}{2a}\lt0$,即抛物线的对称轴在$y$轴左侧;反之当$a$,$b$异号时,抛物线的对称轴在$y$轴右侧,简记为“左同右异”.
3.「2025重庆开州月考」若点$A(-\frac{5}{2},y_{1})$,$B(-\frac{3}{2},y_{2})$,$C(\frac{3}{2},y_{3})$为二次函数$y = -x^{2}-2x + 1$图象上的三点,则$y_{1}$,$y_{2}$,$y_{3}$的大小关系为
$y_{2}\gt y_{1}\gt y_{3}$
。
答案:答案 $y_{2}\gt y_{1}\gt y_{3}$
解析 抛物线解析式配方成顶点式为$y=-(x + 1)^{2}+2$,$\because a=-1\lt0$,$\therefore$ 抛物线开口向下,对称轴是直线$x=-1$,离对称轴越远,函数值越小.$\because -1-(-\frac{5}{2}) = 1.5$,$-1-(-\frac{3}{2}) = 0.5$,$\frac{3}{2}-(-1)=2.5$,$0.5\lt1.5\lt2.5$,$\therefore y_{2}\gt y_{1}\gt y_{3}$.
4. 已知抛物线$y = x^{2}+4x - 1$,将抛物线向右平移5个单位长度,再向上平移1个单位长度,则新图象与$y$轴的交点坐标为
$(0,5)$
。
答案:答案 $(0,5)$
解析 $\because y=x^{2}+4x - 1=(x + 2)^{2}-5$,$\therefore$ 将抛物线向右平移5个单位长度,再向上平移1个单位长度,所得抛物线的解析式为$y=(x + 2 - 5)^{2}-5 + 1$,即$y=(x - 3)^{2}-4$.当$x = 0$时,$y = 5$.故答案为$(0,5)$.
5.「2025北京西城期中」已知二次函数$y = x^{2}-2x - 3$。
(1) 将$y = x^{2}-2x - 3化成y = a(x - h)^{2}+k$的形式,并写出抛物线的开口方向、对称轴和顶点坐标。
(2) 直接写出当$-1 < x < 2$时,函数值$y$的取值范围。
答案:解析 (1)$y=x^{2}-2x - 3=x^{2}-2x + 1 - 1 - 3=(x - 1)^{2}-4$.
抛物线开口向上,对称轴为直线$x = 1$,顶点坐标是$(1,-4)$.
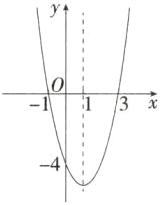
(2)如图,画出函数图象,由图象可知,当$-1\lt x\lt2$时,函数值$y$的取值范围为$-4\leqslant y\lt0$.
6.「2025浙江杭州萧山期中」如图所示的是二次函数$y = ax^{2}+bx + c$图象的一部分,其对称轴为直线$x = -1$,且过点$(-3,0)$。下列说法:①$abc < 0$;②$2a + b = 0$;③$a + b + c = 0$;④若$(-5,y_{1})$,$(2,y_{2})$是抛物线上的两点,则$y_{1} > y_{2}$。其中说法正确的个数是(
C
)

A. 1
B. 2
C. 3
D. 4
答案:C $\because$ 二次函数的图象开口向上,$\therefore a\gt0$,$\because$ 二次函数的图象与$y$轴的交点在负半轴上,$\therefore c\lt0$,$\because$ 对称轴是直线$x=-1$,$\therefore -\frac{b}{2a}=-1$,$\therefore b = 2a\gt0$,$\therefore abc\lt0$,$2a - b = 0$,故①说法正确,②说法不正确;$\because$ 对称轴为直线$x=-1$,且过点$(-3,0)$,$\therefore$ 图象一定过点$(1,0)$,则$a + b + c = 0$,故③说法正确;由题图得,当$x\gt - 1$时,$y$随$x$的增大而增大,$\because (-5,y_{1})$关于直线$x=-1$的对称点的坐标是$(3,y_{1})$,$3\gt2$,$\therefore y_{1}\gt y_{2}$,故④说法正确.综上所述,正确的结论有3个.故选C.
7.「2025上海浦东惠南学区月考,★☆」已知抛物线$y = ax^{2}+bx + c(a \neq 0)上部分点的横坐标x和纵坐标y$的对应值如下表:

根据表格,下列判断正确的是(
C
)
A. 该抛物线开口向上
B. 在对称轴左侧,$y随x$的增大而减小
C. 该抛物线一定经过点$(-1,-\frac{15}{2})$
D. 该抛物线的对称轴是直线$x = 1$
答案:C 由题表中点$(0,-5)$,$(4,-5)$,可知函数图象的对称轴为直线$x = 2$,故D错误;由题表数据可知,当$x\gt2$时,$y$随$x$的增大而减小,当$x\lt2$时,$y$随$x$的增大而增大,故抛物线$y = ax^{2}+bx + c$的开口向下,故A、B错误;点$(5,-\frac{15}{2})$关于直线$x = 2$的对称点为$(-1,-\frac{15}{2})$,$\therefore$ 该抛物线一定经过点$(-1,-\frac{15}{2})$,故C正确.故选C.
8.「2024四川乐山中考,★☆」已知二次函数$y = x^{2}-2x(-1 \leq x \leq t - 1)$,当$x = -1$时,函数取得最大值;当$x = 1$时,函数取得最小值,则$t$的取值范围是(
C
)
A. $0 < t \leq 2$
B. $0 < t \leq 4$
C. $2 \leq t \leq 4$
D. $t \geq 2$
答案:C $\because y=x^{2}-2x=(x - 1)^{2}-1$,$\therefore$ 抛物线的对称轴为直线$x = 1$,且顶点坐标为$(1,-1)$.$\because 1-(-1)=3 - 1$,$\therefore x=-1$和$x = 3$时的函数值相等.$\because -1\leqslant x\leqslant t - 1$,当$x=-1$时,函数取得最大值,$\therefore t - 1\leqslant3$,又$\because$ 当$x = 1$时,函数取得最小值,$\therefore t - 1\geqslant1$,$\therefore 1\leqslant t - 1\leqslant3$,解得$2\leqslant t\leqslant4$.故选C.