答案：10. C ①$\because $函数图象开口向上,$\therefore a＞0$,∵对称轴在y轴右侧,∴a、b异号,$\therefore b＜0$,∵抛物线与y轴交点在y轴负半轴上,$\therefore c＜0,\therefore bc＞0$,故①错误;②$\because $二次函数$y=ax^{2}+bx+c$的图象与x轴交于点$A(3,0)$,与y轴交于点B,对称轴为直线$x = 1,\therefore -\frac {b}{2a}=1$,抛物线与x轴的另一交点为$(-1,0),\therefore b=-2a,a - b + c = 0,\therefore 3a + c = 0,\therefore 3a + 2c＜0$,故②正确;③$\because $抛物线对称轴为直线$x = 1,a＞0,\therefore ax^{2}+bx+c\geq a + b + c$,即$ax^{2}+bx\geq a + b$,故③正确;④$\because (-1)\times3=-3=\frac {c}{a},\therefore c=-3a,\because -2＜c＜-1,\therefore -2＜-3a＜-1,\therefore \frac {1}{3}＜a＜\frac {2}{3},\because b=-2a,\therefore a + b + c=a - 2a - 3a=-4a,\therefore -\frac {8}{3}＜a + b + c＜-\frac {4}{3}$,故④正确.综上所述,正确的有②③④.故选C.

答案：11. 答案 $\frac {1}{2}$解析 $\because $点$A(-2,1)$与点$B(a,b)$关于原点对称,$\therefore a = 2,b = -1,\therefore a^{b}=2^{-1}=\frac {1}{2}$.

答案：12. 答案 $y=-x^{2}+1$（答案不唯一）解析 由题意得$b = 0,a＜0,c＞0,\therefore $这个二次函数的解析式可以是$y=-x^{2}+1$. (答案不唯一)

答案：13. 答案 $-1＜x＜3$解析 由题图可知抛物线与x轴的一个交点坐标是$(-1,0)$,对称轴为直线$x = 1,\therefore $抛物线与x轴的另一交点坐标为$(3,0),\therefore $当$y＞0$时,$-1＜x＜3,\therefore $关于x的不等式$ax^{2}+bx+c＞0$的解集为$-1＜x＜3$.

答案：14. 答案 $\frac {3}{5}$解析 $\because $盒中有x枚黑棋和y枚白棋,$\therefore $共有$(x + y)$枚棋,$\because $从盒中随机取出一枚棋是黑棋的概率是$\frac {3}{8}$,$\therefore $可得关系式$\frac {x}{x + y}=\frac {3}{8},\therefore 8x = 3x + 3y$,即$5x = 3y,\therefore \frac {x}{y}=\frac {3}{5}$.

答案：15. 答案 $80^{\circ }$或$100^{\circ }$解析 $\because ∠BPC=130^{\circ },\therefore ∠PBC+∠PCB=180^{\circ }-130^{\circ }=50^{\circ },\because BP$平分$∠ABC$,CP平分$∠ACB,\therefore ∠ABC=2∠PBC,∠ACB=2∠PCB,\therefore ∠ABC+∠ACB=2(∠PBC+∠PCB)=100^{\circ },\therefore ∠BAC=180^{\circ }-100^{\circ }=80^{\circ }$,当M在优弧BC上时,$∠BMC=∠BAC=80^{\circ }$,当M在劣弧BC上时,由圆内接四边形的性质得$∠BMC=180^{\circ }-80^{\circ }=100^{\circ },\therefore ∠BMC=80^{\circ }$或$100^{\circ }$.

答案：16. 答案 $\frac {4}{3}$解析 $\because $实数a、b分别满足$a^{2}-4a + 3 = 0,b^{2}-4b + 3 = 0$,且$a≠b,\therefore a$、b可看作方程$x^{2}-4x + 3 = 0$的两个不相等的实数根,则$a + b = 4,ab = 3$,则原式$=\frac {a + b}{ab}=\frac {4}{3}$.

答案：17. 答案 $-\frac {3}{5}$解析 将$A(0,m),B(1,-m),D(3,-m)$代入$y=ax^{2}+bx+c(a≠0)$,得$\left\{\begin{array}{l} c = m\\ a + b + c = -m\\ 9a + 3b + c = -m\end{array}\right. $,$\therefore \left\{\begin{array}{l} a=\frac {2}{3}m\\ b=-\frac {8}{3}m\\ c = m\end{array}\right. $,$\therefore y=\frac {2}{3}mx^{2}-\frac {8}{3}mx + m$,把$C(2,n)$代入$y=\frac {2}{3}mx^{2}-\frac {8}{3}mx + m$,得$n=\frac {2}{3}m\times2^{2}-\frac {8}{3}m\times2 + m,\therefore n=-\frac {5}{3}m,\therefore \frac {m}{n}=-\frac {3}{5}$.

答案：
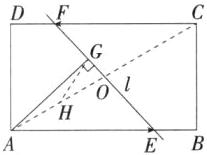
18. 答案 1解析 连接AC,交EF于点O,取OA的中点H,连接GH,如图所示. $\because $四边形ABCD是矩形,$\therefore ∠ABC=90^{\circ },AB// CD,\therefore $在$Rt△ABC$中,$AC=\sqrt {AB^{2}+BC^{2}}=\sqrt {(\sqrt {3})^{2}+1^{2}}=2,\because AB// CD,\therefore ∠EAO=∠FCO,∠AEO=∠CFO$,在$△AOE$与$△COF$中,$\left\{\begin{array}{l} ∠EAO=∠FCO\\ AE = CF\\ ∠AEO=∠CFO\end{array}\right. $,$\therefore △AOE\cong △COF(ASA),\therefore OA=OC=\frac {1}{2}AC=1,\because AG⊥EF$,H是OA的中点,$\therefore GH=\frac {1}{2}AO=\frac {1}{2},\therefore G$的轨迹为以H为圆心,$\frac {1}{2}$为半径,即AO为直径的圆弧.$\therefore AG$的最大值为AO的长,即$AG_{max}=AO=1$.

答案：19. 解析 (1)移项,得$x^{2}-4x=-1$,配方,得$x^{2}-4x + 4=-1 + 4$,即$(x - 2)^{2}=3$,开平方,得$x - 2=\pm \sqrt {3}$,解得$x_{1}=2+\sqrt {3},x_{2}=2-\sqrt {3}$. ………………… (3分)(2)原方程整理得$x(2x - 5)-2(2x - 5)=0$,提公因式,得$(2x - 5)(x - 2)=0,\therefore 2x - 5 = 0$或$x - 2 = 0$,解得$x_{1}=\frac {5}{2},x_{2}=2$. …………………………… (6分)