1.「2024 甘肃甘南州中考」中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是 (
D
)

答案:期末综合检测
1. D 根据中心对称图形的定义,可知A,B,C选项不符合题意,D选项符合题意.故选D.
2.跨语文古诗词「2025 重庆开州期中」下列诗句所描述的事件中,是不可能事件的是 (
A
)
A.手可摘星辰
B.黄河入海流
C.大漠孤烟直
D.鱼戏莲叶东
答案:2. A A.手可摘星辰是不可能事件,符合题意;B.黄河入海流是必然事件,不符合题意;C.大漠孤烟直是随机事件,不符合题意;D.鱼戏莲叶东是随机事件,不符合题意.故选A.
3.「2024 四川凉山州中考」若关于 $ x $ 的一元二次方程 $ (a + 2)x^2 + x + a^2 - 4 = 0 $ 的一个根是 $ x = 0 $,则 $ a $ 的值为 (
A
)
A.2
B.-2
C.2 或-2
D.$\frac{1}{2}$
答案:3. A ∵关于x的一元二次方程$(a+2)x^{2}+x+a^{2}-4=0$的一个根是$x=0,\therefore a^{2}-4=0$且$a+2≠0$,解得$a=2$.故选A.
4.「2025 北京大兴期末」如图,在 $ \triangle ABC $ 中,$ \angle CAB = 70^\circ $,在同一平面内,将 $ \triangle ABC $ 绕点 $ A $ 逆时针旋转 $ \alpha $ 得到 $ \triangle AB'C' $,且 $ C'C // AB $,则 $ \alpha $ 的度数为 (
C
)

A.20°
B.35°
C.40°
D.55°
答案:4. C $\because C'C// AB,\therefore ∠ACC'=∠CAB=70^{\circ },\because $将$△ABC$绕点A逆时针旋转α得到$△AB'C',\therefore AC=AC'$,$∠BAB'=∠CAC'=α,\therefore ∠ACC'=∠AC'C=70^{\circ },\therefore ∠CAC'=40^{\circ }=α$.故选C.
5.「2024 内蒙古赤峰中考」如图,$ AD $ 是 $ \odot O $ 的直径,$ AB $ 是 $ \odot O $ 的弦,半径 $ OC \perp AB $,连接 $ CD $,交 $ OB $ 于点 $ E $,$ \angle BOC = 42^\circ $,则 $ \angle OED $ 的度数是 (
B
)

A.61°
B.63°
C.65°
D.67°
答案:5. B $\because $半径$OC⊥AB,\therefore \widehat {AC}=\widehat {BC},\therefore ∠AOC=∠BOC=42^{\circ },\therefore ∠D=\frac {1}{2}∠AOC=21^{\circ },\because OC=OD,\therefore ∠C=∠D=21^{\circ },\therefore ∠OED=∠C+∠BOC=21^{\circ }+42^{\circ }=63^{\circ }$.故选B.
6.「2025 辽宁丹东期末」如图,公园里有一段长 20 米的墙 $ AB $,工人师傅计划利用墙 $ AB $ 和 40 米长的栅栏围成一个面积为 198 平方米的封闭矩形绿化区域,设矩形中垂直于墙 $ AB $ 的一边的栅栏长为 $ x $ 米,下列说法正确的是 (
C
)

A.$ 2x \cdot (40 - 2x) = 198 $
B.$ x $ 的取值范围是 $ 0 < x \leq 20 $
C.只有一种围法
D.有两种围法
答案:6. C $\because $垂直于墙的一边的栅栏长为x米,$\therefore $平行于墙的一边的栅栏长为$(40-2x)$米,则$x(40-2x)=198$,故A错误;由题意得$\left\{\begin{array}{l} x>0\\ 0<40 - 2x\leq20\end{array}\right. $,解得$10\leq x<20$,故B错误;对于方程$x(40-2x)=198$,化简得$x^{2}-20x+99=0$,解方程得$x_{1}=9,x_{2}=11,\because 10\leq x<20,\therefore x=11$,故只有一种围法,故C正确、D错误.故选C.
7.「2025 吉林长春期末」已知一个二次函数 $ y = ax^2 + bx + c $ 的自变量 $ x $ 与函数 $ y $ 的几组对应值如表:

则下列关于这个二次函数的结论正确的是 (
C
)
A.图象的开口向下
B.表格中 $ m $ 的值大于零
C.函数的最小值是$-\frac{5}{4}$
D.当 $ x > 1 $ 时,$ y $ 的值随 $ x $ 值的增大而增大
答案:7. C 将$(-1,5),(0,1),(1,-1)$代入$y=ax^{2}+bx+c$得$\left\{\begin{array}{l} a - b + c = 5\\ c = 1\\ a + b + c = -1\end{array}\right. $,解得$\left\{\begin{array}{l} a = 1\\ b = -3\\ c = 1\end{array}\right. $,$\therefore y=x^{2}-3x+1$.A.$\because a = 1>0,\therefore $该抛物线开口向上,故该选项结论错误,不符合题意;B.当$x = 2$时,$y=m=4 - 6 + 1=-1<0$,故该选项结论错误,不符合题意;C.$y_{最小值}=\frac {4 - 9}{4}=-\frac {5}{4}$,故该选项结论正确,符合题意;D.抛物线的对称轴为直线$x=\frac {3}{2},\because a = 1>0,\therefore $当$x>\frac {3}{2}$时,y随x的增大而增大,故该选项结论错误,不符合题意.故选C.
8.新考向新定义题对于实数 $ a,b $ 定义运算“$ \otimes $”为 $ a \otimes b = b^2 - ab $,例如 $ 3 \otimes 2 = 2^2 - 3 × 2 = -2 $,则关于 $ x $ 的方程 $ (k - 3) \otimes x = k - 1 $ 的根的情况,下列说法正确的是 (
A
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.无法确定
答案:8. A $\because (k - 3)\otimes x=k - 1,\therefore x^{2}-(k - 3)x=k - 1,\therefore x^{2}-(k - 3)x - k + 1=0,\therefore \Delta=[-(k - 3)]^{2}-4\times1\times(-k + 1)=(k - 1)^{2}+4>0,\therefore $关于x的方程$(k - 3)\otimes x=k - 1$有两个不相等的实数根.故选A.
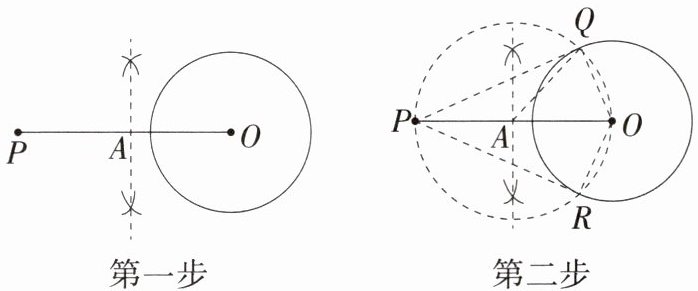
9.「2025 北京通州期末」如图,已知 $ \odot O $ 及 $ \odot O $ 外一定点 $ P $,嘉嘉同学进行了如图所示的两步操作后,得出了四个结论:
①点 $ A $ 是 $ PO $ 的中点;
②直线 $ PQ,PR $ 都是 $ \odot O $ 的切线;
③点 $ P $ 到点 $ Q $、点 $ R $ 的距离相等;
④$ S_{\triangle PQA} = \frac{1}{8}S_{四边形PROQ} $.其中正确的是 (
B
)
A.①②③④
B.①②③
C.①
D.②
答案:9. B 第一步作出的虚线是线段OP的垂直平分线,∴点A是PO的中点,①中结论正确;第二步中,由圆周角定理可知$∠OQP=∠ORP=90^{\circ },\therefore $直线PQ,PR都是$\odot O$的切线,②中结论正确;由切线长定理可知$PQ = PR$,③中结论正确;由A是PO的中点得$S_{\triangle PQA}=\frac {1}{2}S_{\triangle OQP}$,由题意易得$S_{\triangle POQ}=S_{\triangle POR},\therefore S_{\triangle PQA}=\frac {1}{4}S_{四边形PROQ}$,④中结论错误.故选B.