20.「2024 江苏宿迁中考」(6 分)某校组织七年级学生开展以“讲好红色故事,传承红色基因”为主题的研学活动,策划了四条研学线路供学生选择:A.彭雪枫纪念馆,B.淮海军政大礼堂,C.爱园烈士陵园,D.大王庄党性教育基地,每名学生只能任意选择一条线路.
(1)小刚选择线路 A 的概率为
$\frac{1}{4}$
.
(2)请用画树状图或列表的方法,求小刚和小红选择同一线路的概率.
小红小刚
A B C D A (A,A) (A,B) (A,C) (A,D) B (B,A) (B,B) (B,C) (B,D) C (C,A) (C,B) (C,C) (C,D) D (D,A) (D,B) (D,C) (D,D)共有16种等可能的结果,其中小刚和小红选择同一线路的结果有4种,$\therefore $小刚和小红选择同一线路的概率为
$\frac{1}{4}$
.
答案:20. 解析 (1)$\frac {1}{4}$. …………………………… (2分)(2)列表如下:____ A B C D A (A,A) (A,B) (A,C) (A,D) B (B,A) (B,B) (B,C) (B,D) C (C,A) (C,B) (C,C) (C,D) D (D,A) (D,B) (D,C) (D,D)共有16种等可能的结果,其中小刚和小红选择同一线路的结果有4种,$\therefore $小刚和小红选择同一线路的概率为$\frac {4}{16}=\frac {1}{4}$. …… (6分)
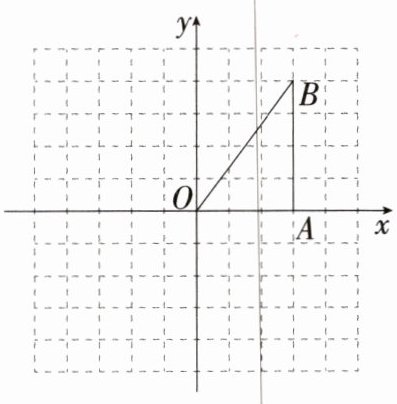
21.(8 分)如图所示的方格纸(1 格长为一个单位长度)中,$ \triangle AOB $ 的顶点坐标分别为 $ A(3,0),O(0,0),B(3,4) $.
(1)将 $ \triangle AOB $ 沿 $ x $ 轴向左平移 5 个单位,画出平移后的 $ \triangle A_1O_1B_1 $(不写作法,但要标出顶点字母).
(2)将 $ \triangle AOB $ 绕点 $ O $ 顺时针旋转 $ 90^\circ $,画出旋转后的 $ \triangle A_2O_2B_2 $(不写作法,但要标出顶点字母).
(3)在(2)的条件下,求点 $ B $ 绕点 $ O $ 旋转到点 $ B_2 $ 所经过的路径长(结果保留 $ \pi $).
答案:21. 解析 (1)如图,$△A_{1}O_{1}B_{1}$即为所求.

……………………………… (2分)(2)如图,$△A_{2}O_{2}B_{2}$即为所求. ……………… (4分)(3)由图可知,点B绕点O旋转到点$B_{2}$所经过的路径是弧$BB_{2}$,在$Rt△AOB$中,$OB=\sqrt {OA^{2}+AB^{2}}=5,\therefore $路径长$=\frac {90}{360}×2π×5=\frac {5}{2}π$. ……………… (8分)
22.「2023 湖南郴州中考」(8 分)如图,在 $ \odot O $ 中,$ AB $ 是直径,点 $ C $ 是圆上一点.在 $ AB $ 的延长线上取一点 $ D $,连接 $ CD $,使 $ \angle BCD = \angle A $.
(1)求证:直线 $ CD $ 是 $ \odot O $ 的切线.
(2)若 $ \angle ACD = 120^\circ,CD = 2\sqrt{3} $,求图中阴影部分的面积(结果用含 $ \pi $ 的式子表示).

答案:22. 解析 (1)证明:连接OC,

$\because AB$是直径,$\therefore ∠ACB=∠OCA+∠OCB=90^{\circ }$. …………… (2分)$\because OA=OC,∠BCD=∠A,\therefore ∠OCA=∠A=∠BCD,\therefore ∠BCD+∠OCB=∠OCD=90^{\circ },\therefore OC⊥CD$. ………………………………… (3分)$\because OC$是$\odot O$的半径,$\therefore $直线CD是$\odot O$的切线. ………………… (4分)(2)$\because ∠ACD=120^{\circ },∠ACB=90^{\circ },\therefore ∠A=∠BCD=120^{\circ }-90^{\circ }=30^{\circ },\therefore ∠BOC=2∠A=60^{\circ }$, ……………………… (5分)$\therefore ∠D=90^{\circ }-∠BOC=90^{\circ }-60^{\circ }=30^{\circ },\therefore OD=2OC$,在$Rt△OCD$中,$OC^{2}+CD^{2}=OD^{2}$,即$OC^{2}+(2\sqrt {3})^{2}=4OC^{2}$,解得$OC = 2$(舍负), ………………………… (6分)$\therefore S_{阴影部分}=S_{\triangle OCD}-S_{扇形BOC}=\frac {1}{2}×2\sqrt {3}×2-\frac {60×π×2^{2}}{360}=2\sqrt {3}-\frac {2π}{3}$. ………………………………… (8分)
23.「2025 山东滨州邹平一模」(10 分)某水果批发商销售每箱进价为 40 元的苹果,物价部门规定每箱销售价不得高于 72 元,市场调查发现,若每箱以 50 元的价格销售,平均每天销售 500 箱,每箱价格每提高 1 元平均每天少销售 10 箱.设每箱涨价 $ x $ 元,每天盈利 $ y $ 元.
(1)列出 $ y $ 与 $ x $ 的函数关系式.
(2)若该批发商要盈利 8750 元,则每箱苹果的售价为多少元?
(3)当每箱苹果的售价为多少元时,可获得最大利润? 最大利润是多少?
答案:23. 解析 (1)由题意得$y=(x + 50 - 40)(500 - 10x)$,化简得$y=-10x^{2}+400x + 5000$. …………… (2分)(2)由题意可得$8750=-10x^{2}+400x + 5000$,化简得$(x - 25)(x - 15)=0$,解得$x_{1}=25,x_{2}=15,\because 50 + 25 = 75>72,50 + 15 = 65<72,\therefore $每箱苹果的售价为65元. ………………… (5分)(3)$y=-10x^{2}+400x + 5000=-10(x^{2}-40x + 400 - 400)+5000=-10(x - 20)^{2}+9000,\because -10<0,\therefore $当$x = 20$时,y有最大值,最大值为9000,$\therefore $当每箱苹果的售价为$50 + 20 = 70$元时,可获得最大利润,最大利润是9000元. …………… (10分)