5. 同学们,你们认识多边形的外角吗?多边形的边与它的邻边延长线所形成的夹角就是它的外角。如下图,$∠ 1$、$∠ 2$、$∠ 3$就是三角形的三个外角,$∠ 4$、$∠ 5$、$∠ 6$、$∠ 7$就是四边形的四个外角。
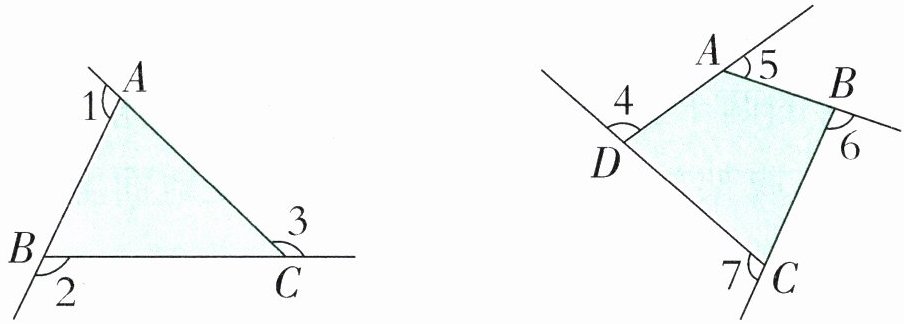
(1)仔细观察每个图形的内角与外角之间的关系,画一画、算一算,想办法推算出每个图形的外角的和各是多少度?
(2)初步得出结论:三角形的三个外角和是(
360
)$^{\circ}$;四边形的四个外角和是(
360
)$^{\circ}$。
(3)根据上面的发现,你有什么猜想?
答案:5. (1)三角形:$3×180^{\circ}-180^{\circ}=360^{\circ}$
四边形:$4×180^{\circ}-360^{\circ}=360^{\circ}$
(2)$360$ $360$
(3)多边形的外角和是 $360^{\circ}$。
【提示】利用“内角 + 相邻外角 $=180^{\circ}$,先算内角与外角度数总和,再减去内角和,得到外角和。
如右下图所示,在$△ ABC$中,$∠ 1=∠ 2+5^{\circ}$,$∠ 3=∠ 4+5^{\circ}$,$∠ 5=130^{\circ}$,$∠ A$等于多少度?
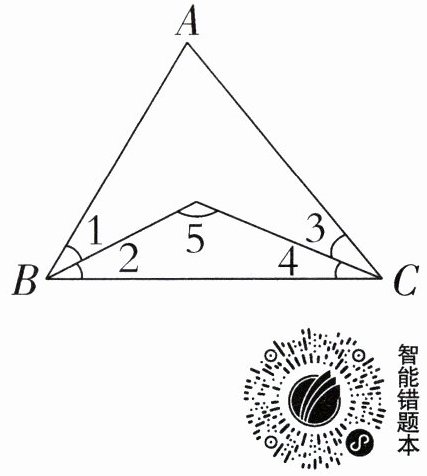
答案:附加题
$∠2+∠4 = 180^{\circ}-130^{\circ}=50^{\circ}$
$∠1+∠3=∠2 + 5^{\circ}+∠4 + 5^{\circ}=60^{\circ}$
$∠ A = 180^{\circ}-50^{\circ}-60^{\circ}=70^{\circ}$
【提示】三角形内角和等于 $180^{\circ}$。