3. 小美、小明和小丽三人分桃,小美分得了总数的一半多5个,小明分得了剩下的一半少2个,还有14个分给了小丽。一共有多少个桃?
答案:3. $(14 - 2)×2 = 24$ (个) $(24 + 5)×2 = 58$ (个) 【提示】可以从最后小丽分得的桃子数量入手,逐步往前推算出桃子的总数。
解析:
$(14 - 2)×2 = 24$ (个)
$(24 + 5)×2 = 58$ (个)
答:一共有58个桃。
4. 王大伯家有一块长方形菜地,如果长增加8米,或者宽增加6米,那么面积都比原来增加72平方米。王大伯家长方形菜地的面积是多少平方米?(先在正确的示意图下面画“√”,再计算)
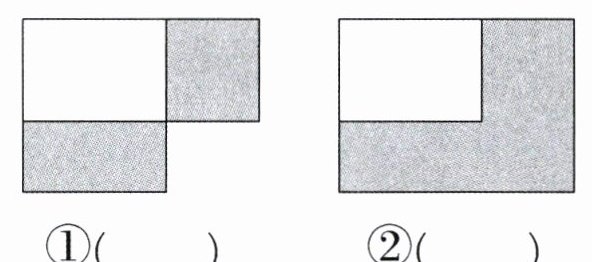
答案:4. ①(√) $(72÷8)×(72÷6) = 108$ (平方米) 【提示】长增加 8 米或宽增加 6 米,增加部分是长方形。图①能体现长增加、宽增加时面积的变化,所以①(√)。长增加 8 米时,面积增加 72 平方米,根据长方形面积公式,原来的宽 $= 72÷8 = 9$ (米)。宽增加 6 米时,面积增加 72 平方米,原来的长 $= 72÷6 = 12$ (米)。原长方形面积 = 长×宽,即 $12×9 = 108$ (平方米)。
解析:
①(√)
原来的宽:$72÷8 = 9$(米)
原来的长:$72÷6 = 12$(米)
面积:$12×9 = 108$(平方米)
5. 右下图是一块正方形草坪,如果把它的边长增加3米,那么草坪的面积就增加81平方米。现在草坪的面积是多少平方米?
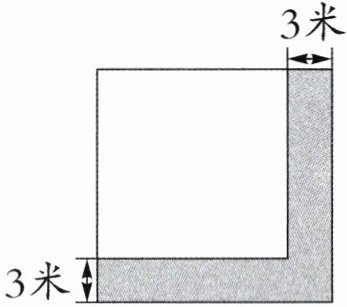
答案:5. 原来草坪的边长:$(81 - 3×3)÷2÷3 = 12$ (米) 现在草坪的面积:$12×12 + 81 = 225$ (平方米) 【提示】增加的 81 平方米,是由三部分组成的,第一部分是面积为 $3×3 = 9$ (平方米)的小正方形,第二、三部分是 2 个宽是 3 米、长等于原来正方形边长的长方形,由此可求出原来正方形的边长是 $(81 - 3×3)÷2÷3 = 12$ (米),用原来草坪的面积加上增加的面积即可求出现在草坪的面积。
解析:
原来草坪的边长:$(81 - 3×3)÷2÷3 = 12$ (米)
现在草坪的面积:$12×12 + 81 = 225$ (平方米)
6. 小军和小明的钱数相等,小军用去80元,小明用去280元,小军剩下的钱数是小明的3倍。小军和小明各剩下多少元?
答案:6. 小明剩下的钱:$(280 - 80)÷(3 - 1) = 100$ (元) 小军剩下的钱:$100×3 = 300$ (元) 【提示】根据题意画出线段图如下:
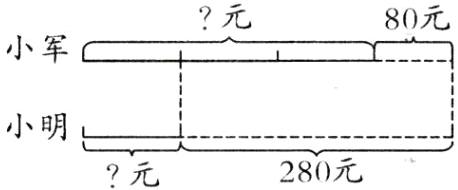
书架的上、中、下三层共放书226本,其中上层的本数比其余两层所放书的本数之和少38,而中层比下层又多放了4本,则上、中、下三层各放书多少本?

答案:上层:$(226 - 38)÷2 = 94$ (本)
中层和下层共:$226 - 94 = 132$ (本)
中层:$(132 + 4)÷2 = 68$ (本)
下层:$(132 - 4)÷2 = 64$ (本)
【提示】根据三层共放书 226 本,上层的本数比其余两层所放书的本数之和少 38,用解决和差问题的方法求出上层放书的本数,进而求出中层和下层放书的总本数。根据中层比下层又多放了 4 本,再次用解决和差问题的方法分别求出中层和下层放书的本数。