1. 新考法 开放探究 学习了三角形与四边形的内角和之后,甲、乙和丙三位同学一起探索六边形的内角和,他们的思考过程如下图。
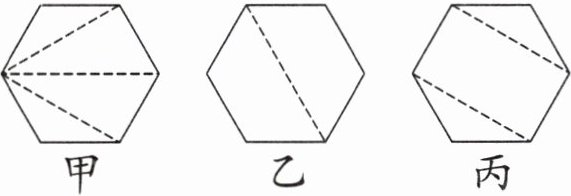
(1)我明白(
)的想法,根据他的想法,请列式计算六边形的内角和:(
)。
(2)小亮在探究六边形的内角和时,他列式为“$180^{\circ}×6 - 360^{\circ}$”,请把他的想法在下面的六边形里表示出来。
答案:1. (1)甲 $180^{\circ} × 4=720^{\circ}$
或乙 $360^{\circ} × 2=720^{\circ}$
或丙 $180^{\circ} × 2+360^{\circ}=720^{\circ}$
(2)

(画法不唯一)
【提示】$180^{\circ} × 6$表示小亮把六边形分成6个三角形,通过分一分发现,中间的角不是六边形的内角,它们组成了一个周角,要减去才行。
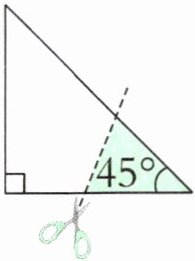
2. 如右图,沿虚线剪去一张等腰直角三角形纸片的涂色部分。剩下图形的内角和是(
D
)。
A.$135^{\circ}$
B.$180^{\circ}$
C.$270^{\circ}$
D.$360^{\circ}$
答案:2. D 【提示】剩下的部分是四边形,四边形的内角和是$360^{\circ}$。
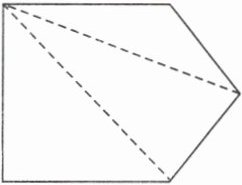
3. 小文在探索五边形的内角和时,把一个五边形进行了分割(如图)。下面选项中,(
C
)体现了他的推算过程。
A.$180^{\circ}×5$
B.$180^{\circ}×3 + 360^{\circ}$
C.$180^{\circ}×3$
D.$180^{\circ}×5 - 180^{\circ}$
答案:3. C 【提示】小文把五边形分成了3个三角形,所以五边形的内角和是$180^{\circ} × 3=540^{\circ}$。
4. 分一分,画一画,你能算出右下图的内角和吗?
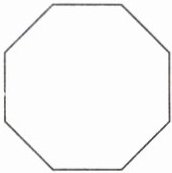
答案:4.
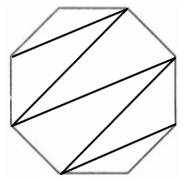
$180^{\circ} × (8-2)=1080^{\circ}$
【提示】题图可以分成6个三角形。
5. 乐乐在计算一个多边形的内角和时,少算了一个角,得到内角和是$1230^{\circ}$,少算的角的度数是多少度?这个多边形是几边形?
答案:5. $1230^{\circ} ÷ 180^{\circ}=6······150^{\circ}$
$180^{\circ}-150^{\circ}=30^{\circ}$
$1230^{\circ}+30^{\circ}=1260^{\circ}$
$1260^{\circ} ÷ 180^{\circ}+2=9$(条)
少算的角是$30^{\circ}$,这个多边形是九边形。
【提示】多边形可以分成三角形来计算内角和,且内角和应是$180^{\circ}$的倍数,$1230^{\circ} ÷ 180^{\circ}=6······150^{\circ}$,因为少算了一个角,少算的角的度数是$180^{\circ}-150^{\circ}=30^{\circ}$,这个多边形的内角和应是$1230^{\circ}+30^{\circ}=1260^{\circ}$,$1260^{\circ} ÷ 180^{\circ}+2=9$(条),这个多边形是九边形。
6. 实验班原创 几何直观 一个梯形,把它剪去一个角后,剩下的部分内角和可能是多少?先画一画,再计算。
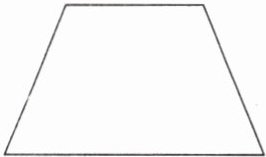
答案:6.

(画法不唯一)
可能是$180^{\circ}$、$360^{\circ}$或$540^{\circ}$。
【提示】剩下的部分可能是三角形、四边形或五边形。