1. 下面哪组长度的线段可以围成三角形?在括号里画“√”。
(1) 3 cm 6 cm 9 cm (
)
(2) 4 cm 4 cm 9 cm (
)
(3) 3 cm 7 cm 9 cm (
√
)
(4) 9 cm 9 cm 9 cm (
√
)
答案:1. (1) ( ) (2) ( ) (3) (√) (4) (√)
【提示】三角形任意两边长度的和
大于第三边。
2. 要判断三条线段能否围成一个三角形,只要其中(
B
)的长度和大于第三条边就可以了。
A.较长的两条边
B.较短的两条边
C.最长和最短的两条边
答案:2. B 【提示】三角形只要较短的两条边的长度和大于第三条边,就可以保证任意两边长度的和大于第三边。
3. 比一比,在$◯$里填“>”或“<”。
$a + b◯ c$
$b + c◯ a$
$a + c◯ b$
$a - c◯ b$
$a - b◯ c$
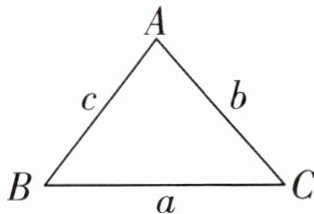
答案:3. > > > < < 【提示】三角形中,任意两边长度的和大于第三边,任意两边长度的差小于第三边。
4. 小明从家上学走哪条路最近?用水彩笔画出来,并说说你的理由。
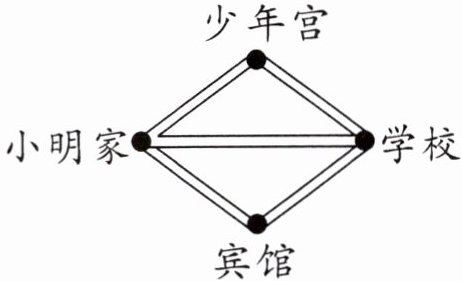
答案:4. 画图略。走中间的那条路最近,因为三角形任意两边长度的和大于第三边。
【提示】三角形任意两边长度的和大于第三边。
5. 三条线段分别长 8 cm、9 cm、14 cm,能否围成三角形呢?
(1) 我来分别试一试。
(
8
)+(
9
)>(
14
)
(
8
)+(
14
)>(
9
)
(
9
)+(
14
)>(
8
)
(2) 你发现了什么规律呢?
我发现只加一次就行了。
(
8
)+(
9
)>(
14
)
只需要把较(
短
)的两边相加,和大于第三边就行了。
答案:5. (1) 8 9 14 8 14 9 9 14 8
(2) 8 9 14 短 【提示】三角形任意两边长度的和大于第三边。
6. 实验班原创 几何直观 一根长 11 厘米的铁丝,要把它分成三段,再首尾相连拼成一个三角形。李鑫在 2 厘米处剪了一刀,再在哪个刻度处剪一刀就能围成一个三角形?请你先在图中标出剪的位置,再把想法写下来。(边长为整厘米数)
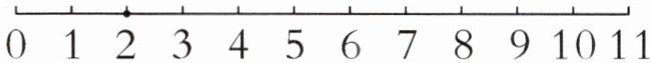
答案:6.
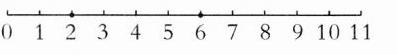
(或在 7 cm 处剪一刀)
想法略,合理即可。
【提示】题中在 2 cm 处剪了一刀,说明三角形有一边是 2 cm,另外两边之和是 11 - 2 = 9(cm)。需要满足任意两边之和大于第三边,还要满足任意两边之差小于第三边,说明两边之差只能是 1 cm,所以另外两边的长度是 4 cm 和 5 cm。
思路引导
引导法
利用三角形的三边关系即三角形任意两边长度的和大于第三边,三角形任意两边长度的差小于第三边的原则确定未知边的取值范围。