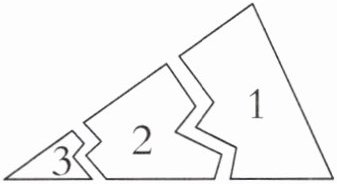
1. 刘刚不小心把一块三角形玻璃打碎成了三块(如下图),现在他要到店里去配一块与原来完全一样的玻璃,那么最省事的办法是带标有序号(
A
)的玻璃碎片去。
A.1
B.2
C.3
答案:1. A 【提示】玻璃碎片1号已知三角形的两个角和一条边,用180°减去这两个角的度数求出第三个角,就可以配出与原来完全一样的玻璃。
2. 下图中所画的4个以AC为底的△ABC、△ADC、△AEC和△AFC的高都是(
3
)厘米。(每个小方格的边长都为1厘米)
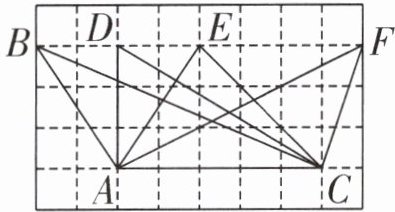
答案:2. 3 【提示】数一数可发现高都是3个小方格的边长和。
3. 数一数,下图中一共有(
10
)个三角形。
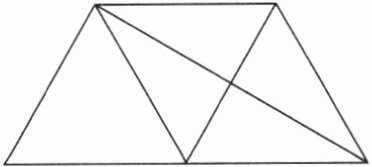
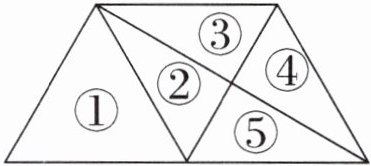
【我思考】第一步,数出基本三角形的个数并标上序号,如下图,有(
5
)个基本三角形。第二步,数出由2个基本三角形组成的三角形有(
4
)个,分别是②+③,②+⑤,③+④,④+⑤。第三步,数出由3个基本三角形组成的三角形有1个,是①+②+⑤。
【我验证】因此一共有(
5+4+1
)=(
10
)个三角形。
【我发现】数图形的数量时,要先数出基本图形的数量,再数出由(
2
)个基本图形组成的这种图形的数量,然后数出由(
3
)个基本图形组成的这种图形的数量……以此类推,直至把所有组合都数出来,最后把所有组合的数量加起来即可。
答案:3. 10 5 4 5+4+1 10 2 3 【提示】数图形的数量时,要先数出基本图形的数量,再数出由2个基本图形组成的这种图形的数量,然后数出由3个基本图形组成的这种图形的数量……以此类推,直至把所有组合都数出来,最后把所有组合的数量加起来即可。
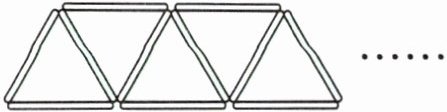
4. 新考法 规律探究 用小棒摆三角形,如下图摆5个三角形要用(
11
)根小棒。照这样摆下去,摆n个三角形要用(
2n+1
)根小棒,77根小棒能摆(
38
)个三角形。
答案:4. 11 2n+1 38 【提示】先分别数出摆1个、2个、3个三角形需要用的小棒数量,观察发现:摆1个三角形用3根小棒,3=2×1+1;摆2个三角形用5根小棒,5=2×2+1;摆3个三角形用7根小棒,7=2×3+1,从而总结出摆n个三角形需要用(2n+1)根小棒。77根小棒能摆的三角形个数:由2n+1=77,先算出2n=76,再求得n=38。
解析:
摆1个三角形用3根小棒,3=2×1+1;摆2个三角形用5根小棒,5=2×2+1;摆3个三角形用7根小棒,7=2×3+1,所以摆n个三角形需要用(2n+1)根小棒。
摆5个三角形:2×5+1=11根。
77根小棒能摆三角形的个数:2n+1=77,2n=76,n=38。
11;2n+1;38