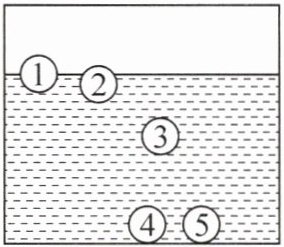
11. (2025·甘肃)小栋了解到伽利略温度计的测温原理后,想自己动手设计一个粗略测温的装置,他的设计思路如下:在密闭的玻璃容器中装上一种密度会随温度升高而减小的特殊液体,液体中有 $ 5 $ 个体积相等、密度不同且标有温度示数的小球,小球不吸收液体且热胀冷缩可以忽略不计,当有小球悬浮时,悬浮小球上标有的温度值就是当前环境的温度。如图所示是这个测温装置的示意图,其中小球 $ 3 $ 上所标温度值为 $ 25 $ ℃。相邻标号的小球上所标的温度值间隔为 $ 2 $ ℃,则下列说法正确的是(
C
)
A.$ 27 $ ℃时,小球 $ 2 $ 处于漂浮状态
B.小球 $ 2 $ 在 $ 27 $ ℃时所受的浮力小于 $ 25 $ ℃时所受的浮力
C.若有 $ 3 $ 个小球漂浮,$ 2 $ 个小球沉底,则环境温度在 $ 23 $ ℃至 $ 25 $ ℃之间
D.若要增大该装置能测得的最高温度,可增加一个与小球 $ 5 $ 体积相等但质量更大的小球
答案:C
12. 如图所示是某型号水下机器人。该机器人可以通过三种方式控制浮沉:第一种是机器人内部水舱充放水,内部水舱的容积率为 $ 4×10^{-3} $ m³;第二种是利用推进器提供竖直向上的推力 $ F_{推} $,$ F_{推} $ 可以在 $ 0~30 $ N 之间调节;第三种是在机器人外部加装不同数量的浮块,每个浮块质量均为 $ 0.4 $ kg、体积均为 $ 1×10^{-3} $ m³。已知该机器人水舱未充水时的质量为 $ 9.5 $ kg,未装浮块时机器人的总体积为 $ 1.2×10^{-2} $ m³(体积不变,含机械臂)。($ \rho_{水}=1.0×10^{3} $ kg/m³,$ g $ 取 $ 10 $ N/kg)
(1)求 $ 150 $ m 深处水的压强。
(2)求当机器人未加浮块、水舱充满水浸没在水中悬停时,$ F_{推} $ 的大小。
(3)深处水底有一物体(未与水底紧密接触),其密度均匀且为 $ 2.5×10^{3} $ kg/m³、体积为 $ 4×10^{-3} $ m³,需机器人潜入水中用机械臂抓住物体打捞上来。为确保打捞顺利进行,机器人下水前需制定好能让机器人抓住物体上浮的方案,在 $ F_{推} $ 调到 $ 30 $ N 的情况下,还需利用另外两种方式才能实现上浮,请通过计算给出一种合理方案。

答案:(1)$1.5×10^{6} Pa$ (2)15 N (3)将水舱中的水全部排出再安装一个浮块 解析:(1)150 m深处水的压强$p=\rho_{水} gh =1.0×10^{3} kg/m^{3}×10 N/kg×150 m=1.5×10^{6} Pa$.(2)机器人水舱未充水时的重力$G_{机}=m_{机}g=9.5 kg×10 N/kg=95 N$,水舱充满水时水的重力$G_{水}=\rho_{水}V_{容}g=1.0×10^{3} kg/m^{3}×4×10^{-3} m^{3}×10 N/kg=40 N$,未装浮块时机器人浸没在水中时所受浮力$F_{浮机}=\rho_{水} V_{机}g=\rho_{水}Vg=1.0×10^{3} kg/m^{3}×1.2×10^{-2} m^{3}×10 N/kg=120 N$,未加浮块、水舱充满水浸没在水中悬停时,机器人受力平衡,则$F_{推}+F_{浮机}=G_{水}+G_{机}$,所以$F_{推}=G_{机}+G_{水}-F_{浮机}=95 N+40 N-120 N=15 N$.(3)物体的重力$G_{物}=m_{物}g=\rho_{物}V_{物}g =2.5×10^{3} kg/m^{3}×4×10^{-3} m^{3}×10 N/kg=100 N$,物体受到的浮力$F_{浮物}=\rho_{水}V_{排物}g=\rho_{水}V_{物}g=1.0×10^{3} kg/m^{3}×4×10^{-3} m^{3}×10 N/kg=40 N$,要把物体打捞上来,机器人的最小拉力$F_{最小}=G_{物}-F_{浮物}=100 N-40 N=60 N$.为确保打捞顺利进行,机器人下水前水舱内先充满水,打捞时排出水舱内全部的水,$F_{推最大}=30 N$,设另外需要安装n个浮块,一个浮块的重力$G_{浮块}=m_{浮块}g=0.4 kg×10 N/kg=4 N$,一个浮块受到的浮力$F_{浮浮块}=\rho_{水} V_{排浮块}g=\rho_{水} V_{浮块}g=1.0×10^{3} kg/m^{3}×1×10^{-3} m^{3}×10 N/kg=10 N$,给物体提供的拉力至少为$F_{最小}=F_{浮机}+F_{推最大}+nF_{浮浮块}-G_{机}-nG_{浮块}=120 N+30 N+n×10 N-95 N-n×4 N=60 N$,解得$n\approx0.83$,n取正整数,则$n=1$,即合理的方案为将水舱中的水全部排出再安装一个浮块.
解析:
(1)$p=\rho_{水}gh=1.0×10^{3}\ \mathrm{kg/m}^{3}×10\ \mathrm{N/kg}×150\ \mathrm{m}=1.5×10^{6}\ \mathrm{Pa}$
(2)$G_{机}=m_{机}g=9.5\ \mathrm{kg}×10\ \mathrm{N/kg}=95\ \mathrm{N}$
$G_{水}=\rho_{水}V_{容}g=1.0×10^{3}\ \mathrm{kg/m}^{3}×4×10^{-3}\ \mathrm{m}^{3}×10\ \mathrm{N/kg}=40\ \mathrm{N}$
$F_{浮机}=\rho_{水}V_{机}g=1.0×10^{3}\ \mathrm{kg/m}^{3}×1.2×10^{-2}\ \mathrm{m}^{3}×10\ \mathrm{N/kg}=120\ \mathrm{N}$
$F_{推}=G_{机}+G_{水}-F_{浮机}=95\ \mathrm{N}+40\ \mathrm{N}-120\ \mathrm{N}=15\ \mathrm{N}$
(3)$G_{物}=\rho_{物}V_{物}g=2.5×10^{3}\ \mathrm{kg/m}^{3}×4×10^{-3}\ \mathrm{m}^{3}×10\ \mathrm{N/kg}=100\ \mathrm{N}$
$F_{浮物}=\rho_{水}V_{物}g=1.0×10^{3}\ \mathrm{kg/m}^{3}×4×10^{-3}\ \mathrm{m}^{3}×10\ \mathrm{N/kg}=40\ \mathrm{N}$
$F_{最小}=G_{物}-F_{浮物}=100\ \mathrm{N}-40\ \mathrm{N}=60\ \mathrm{N}$
$G_{浮块}=m_{浮块}g=0.4\ \mathrm{kg}×10\ \mathrm{N/kg}=4\ \mathrm{N}$
$F_{浮浮块}=\rho_{水}V_{浮块}g=1.0×10^{3}\ \mathrm{kg/m}^{3}×1×10^{-3}\ \mathrm{m}^{3}×10\ \mathrm{N/kg}=10\ \mathrm{N}$
$F_{最小}=F_{浮机}+F_{推最大}+nF_{浮浮块}-G_{机}-nG_{浮块}$
$60\ \mathrm{N}=120\ \mathrm{N}+30\ \mathrm{N}+n×10\ \mathrm{N}-95\ \mathrm{N}-n×4\ \mathrm{N}$
解得$n\approx0.83$,取$n=1$
方案:将水舱中的水全部排出再安装一个浮块