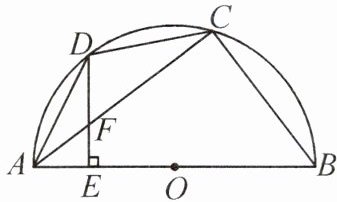
6. 如图,四边形 $ ABCD $ 内接于半圆 $ O $,$ AB $ 为半圆 $ O $ 的直径,$ AD = CD $,过点 $ D $ 作 $ DE ⊥ AB $ 于点 $ E $,连接 $ AC $ 交 $ DE $ 于点 $ F $. 若 $ \sin \angle CAB = \dfrac{3}{5} $,$ DF = 5 $,则 $ BC $ 的长为(
C
)
A.8
B.10
C.12
D.16
答案:6.C 解析:连接$OC$,$OD$,设$OD$与$AC$交于点$G$.因为$AD = CD$,所以$\overset\frown{AD}=\overset\frown{CD}$,所以$\angle AOD = \angle COD$.因为$OA = OC$,所以$AG = CG$,$OG⊥ AC$,所以$\angle DGF = 90^{\circ}$.因为$AB$为半圆$O$的直径,所以$\angle ACB = 90^{\circ}$,所以$\sin\angle CAB =\frac{BC}{AB}=\frac{3}{5}$.设$BC = 3x$,则$AB = 5x$,所以$OA = OD =\frac{1}{2}AB=\frac{5}{2}x$,$AC = \sqrt{AB^{2}-BC^{2}} = 4x$.因为$OA = OB$,所以$OG$是$\triangle ABC$的中位线,所以$OG =\frac{1}{2}BC=\frac{3}{2}x$,所以$DG = OD - OG = x$.因为$\angle FDG + \angle DFG = \angle CAB + \angle AFE = 90^{\circ}$,$\angle DFG = \angle AFE$,所以$\angle FDG = \angle CAB$,所以$\sin\angle FDG = \sin\angle CAB = \frac{3}{5}$.又$\sin\angle FDG =\frac{FG}{DF}$,所以$\frac{FG}{DF}=\frac{3}{5}$.因为$DF = 5$,所以$FG =\frac{3}{5}DF = 3$,所以$DG =\sqrt{DF^{2}-FG^{2}} = 4$,所以$x = 4$,所以$BC = 12$.
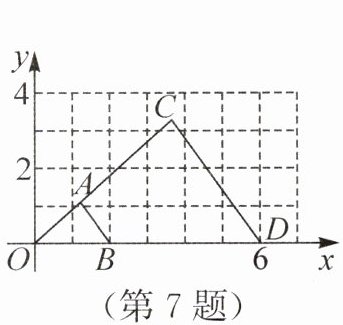
7. (2025·广东)如图,把 $ \triangle AOB $ 放大后得到 $ \triangle COD $,则 $ \triangle AOB $ 与 $ \triangle COD $ 的相似比是
1:3
.
答案:7.$1:3$
解析:
解:由图可知,点$A(2,2)$,$B(2,0)$,$C(4,3)$,$D(6,0)$。
$OB=2$,$OD=6$。
因为$\triangle AOB$放大后得到$\triangle COD$,所以$\triangle AOB ∼ \triangle COD$,相似比为$OB:OD=2:6=1:3$。
$1:3$
8. 新素养
数据观念 如图是小刚一天中的作息时间分配的扇形统计图. 若小刚希望把自己每天的阅读时间调整为 $ 2.5\ \mathrm{h} $,则他的阅读时间需增加
90
$ \mathrm{min} $.

答案:8.$90$
解析:
阅读时间对应的圆心角:$360° - 135° - 120° - 30° - 60° = 15°$
原阅读时间:$\frac{15°}{360°} × 24 = 1\ \mathrm{h}$
需增加时间:$2.5 - 1 = 1.5\ \mathrm{h} = 90\ \mathrm{min}$
90
9. (2024·四川达州)“四大名著”《红楼梦》《水浒传》《三国演义》《西游记》是我国优秀文化的重要组成部分. 某校七年级准备从这四本名著中任意抽取两本(先任意抽取一本,不放回,再任意抽取另一本)开展“名著共读”活动,则该年级的学生恰好抽取到《三国演义》和《西游记》的概率是
$\frac{1}{6}$
.
答案:9.$\frac{1}{6}$
解析:
将四本名著分别记为A(《红楼梦》)、B(《水浒传》)、C(《三国演义》)、D(《西游记》)。
第一次抽取有4种可能,第二次抽取有3种可能,总情况数为$4×3 = 12$种。
恰好抽到《三国演义》和《西游记》的情况有:先抽C再抽D,先抽D再抽C,共2种。
概率为$\frac{2}{12}=\frac{1}{6}$。
$\frac{1}{6}$
10. 对于二次函数 $ y = (x - h)^2 + 1 $($ h $ 为常数),当 $ 1 \leq x \leq 3 $ 时,$ y $ 的最小值为 5,则 $ h = $
-1或5
.
答案:10.$-1$或$5$
解析:
解:二次函数$y=(x - h)^2 + 1$的对称轴为直线$x=h$,开口向上。
当$h < 1$时,在$1 \leq x \leq 3$上,$y$随$x$的增大而增大,$x=1$时$y$取最小值,即$(1 - h)^2 + 1 = 5$,解得$h=-1$或$h=3$(舍去)。
当$h > 3$时,在$1 \leq x \leq 3$上,$y$随$x$的增大而减小,$x=3$时$y$取最小值,即$(3 - h)^2 + 1 = 5$,解得$h=5$或$h=1$(舍去)。
当$1 \leq h \leq 3$时,$y$的最小值为$1$,不符合题意。
综上,$h=-1$或$h=5$。
$-1$或$5$
11. (2025·江苏淮安模拟)如图,在四边形 $
ABC
D $ 中,$ AC $ 与 $ BD $ 相交于点 $ O $,$ \angle ABC = \angle DAC = 90^{\circ} $,$ \tan \angle ACB = \dfrac{1}{2} $,$ \dfrac{OB}{OD} = \dfrac{4}{3} $,则 $ \dfrac{
S_{\triangle ABD}}{S_{\triangle CBD}} = $
$\frac{3}{32}$
.

答案:11.$\frac{3}{32}$ 解析:过点$B$作$BE⊥ AC$于点$E$,则$\angle BEO = \angle BEC = 90^{\circ}$.因为$\angle DAC = 90^{\circ}$,所以$\angle BEO = \angle DAC$.又$\angle EOB = \angle AOD$,所以$\triangle EOB∼ \triangle AOD$,所以$\frac{OE}{OA}=\frac{OB}{OD}=\frac{4}{3}$.因为$\tan\angle ACB = \frac{1}{2}$,所以$\frac{BE}{CE}=\frac{1}{2}$.设$BE = a$,则$CE = 2BE = 2a$.因为$\angle ABC = 90^{\circ}$,所以$\angle ABE + \angle CBE = 90^{\circ}$.又$\angle BCE + \angle CBE = 90^{\circ}$,所以$\angle ABE = \angle BCE$,所以$\triangle ABE∼\triangle BCE$,所以$\frac{AE}{BE}=\frac{BE}{CE}= \frac{1}{2}$,所以$AE =\frac{1}{2}BE=\frac{1}{2}a$,所以$OA =\frac{3}{7}AE = \frac{3}{14}a$,$OE =\frac{4}{7}AE =\frac{2}{7}a$,所以$OC = OE + CE = \frac{16}{7}a$,所以$\frac{OA}{OC}=\frac{3}{32}$,所以$\frac{S_{\triangle AOB}}{S_{\triangle COB}}=\frac{S_{\triangle AOD}}{S_{\triangle COD}}=\frac{OA}{OC}= \frac{3}{32}$,所以$\frac{S_{\triangle AOB}+S_{\triangle AOD}}{S_{\triangle COB}+S_{\triangle COD}}=\frac{3}{32}$,即$\frac{S_{\triangle ABD}}{S_{\triangle CBD}}=\frac{3}{32}$.
解析:
解:过点$B$作$BE ⊥ AC$于点$E$,则$\angle BEO = \angle BEC = 90^{\circ}$。
$\because \angle DAC = 90^{\circ}$,$\angle EOB = \angle AOD$,
$\therefore \triangle EOB ∼ \triangle AOD$,$\therefore \frac{OE}{OA} = \frac{OB}{OD} = \frac{4}{3}$。
$\because \tan \angle ACB = \frac{1}{2}$,$\angle BEC = 90^{\circ}$,
$\therefore \frac{BE}{CE} = \frac{1}{2}$,设$BE = a$,则$CE = 2a$。
$\because \angle ABC = 90^{\circ}$,$\angle ABE + \angle CBE = 90^{\circ}$,$\angle BCE + \angle CBE = 90^{\circ}$,
$\therefore \angle ABE = \angle BCE$,$\therefore \triangle ABE ∼ \triangle BCE$,
$\therefore \frac{AE}{BE} = \frac{BE}{CE} = \frac{1}{2}$,$\therefore AE = \frac{1}{2}BE = \frac{1}{2}a$。
$\because \frac{OE}{OA} = \frac{4}{3}$,设$OA = 3k$,$OE = 4k$,则$AE = OA + OE = 7k = \frac{1}{2}a$,
$\therefore k = \frac{a}{14}$,$\therefore OA = \frac{3a}{14}$,$OE = \frac{4a}{14} = \frac{2a}{7}$。
$\therefore OC = OE + CE = \frac{2a}{7} + 2a = \frac{16a}{7}$,$\therefore \frac{OA}{OC} = \frac{\frac{3a}{14}}{\frac{16a}{7}} = \frac{3}{32}$。
$\because \triangle ABD$与$\triangle CBD$同高,$\therefore \frac{S_{\triangle ABD}}{S_{\triangle CBD}} = \frac{OA}{OC} = \frac{3}{32}$。
答案:$\frac{3}{32}$
12. 如图,把边长为 $ 1:2 $ 的矩形 $ ABCD $ 沿长边 $ BC $,$ AD $ 的中点 $ E $,$ F $ 对折,得到四边形 $ ABEF $,点 $ G $,$ H $ 分别在边 $ BE $,$ EF $ 上,且 $ BG = EH = \dfrac{2}{5}BE = 2 $,连接 $ AG $,$ BH $ 交于点 $ O $,$ N $ 为 $ AF $ 的中点,连接 $ ON $,作 $ OM ⊥ ON $ 交 $ AB $ 于点 $ M $,连接 $ MN $,则 $ \tan \angle AMN = $
$\frac{5}{8}$
.
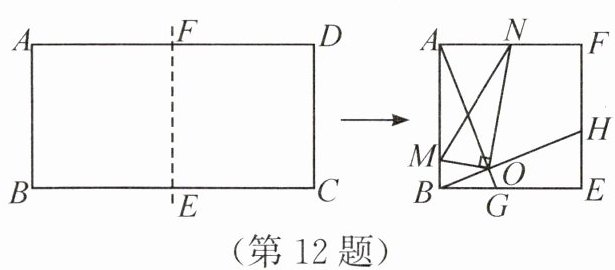
答案:12.$\frac{5}{8}$ 解析:由题意,得四边形$ABEF$是正方形.因为$BG = EH =\frac{2}{5}BE = 2$,所以$AB = AF = BE = 5$.在$\triangle ABG$和$\triangle BEH$中,$\begin{cases}AB = BE, \\ \angle ABG = \angle BEH = 90^{\circ}, \\ BG = EH,\end{cases}$所以$\triangle ABG\cong\triangle BEH$,所以$\angle BAG = \angle EBH$,所以$\angle BAG + \angle ABO = \angle EBH + \angle ABO = \angle ABE = 90^{\circ}$,所以$\angle AOB = 90^{\circ}$,所以$\angle AOM + \angle BOM = 90^{\circ}$,$\tan\angle BAG =\frac{OB}{OA}=\frac{BG}{AB}=\frac{2}{5}$.因为$OM⊥ ON$,所以$\angle MON = 90^{\circ}$,所以$\angle AOM + \angle AON = 90^{\circ}$,所以$\angle BOM = \angle AON$.因为$\angle BAG + \angle OAN = \angle BAF = 90^{\circ}$,所以$\angle ABO = \angle OAN$,所以$\triangle BOM∼\triangle AON$,所以$\frac{BM}{AN}= \frac{OB}{OA}=\frac{2}{5}$.因为$N$为$AF$的中点,所以$AN =\frac{1}{2}AF = \frac{5}{2}$,所以$BM =\frac{2}{5}AN = 1$,所以$AM = AB - BM = 4$,所以$\tan\angle AMN =\frac{AN}{AM}=\frac{5}{8}$.
解析:
解:由题意,四边形$ABEF$是正方形。
因为$BG = EH=\frac{2}{5}BE = 2$,所以$BE=5$,则$AB = AF = BE = 5$。
在$\triangle ABG$和$\triangle BEH$中,
$\begin{cases}AB = BE\\\angle ABG=\angle BEH = 90°\\BG = EH\end{cases}$,
所以$\triangle ABG\cong\triangle BEH$,故$\angle BAG=\angle EBH$。
因为$\angle BAG + \angle ABO=\angle EBH + \angle ABO=\angle ABE = 90°$,
所以$\angle AOB = 90°$,则$\tan\angle BAG=\frac{BG}{AB}=\frac{2}{5}=\frac{OB}{OA}$。
因为$OM⊥ ON$,所以$\angle MON = 90°$,
又$\angle AOB = 90°$,故$\angle BOM=\angle AON$。
因为$\angle BAG + \angle OAN = 90°$,$\angle BAG=\angle EBH=\angle ABO$,
所以$\angle ABO=\angle OAN$,则$\triangle BOM∼\triangle AON$,
所以$\frac{BM}{AN}=\frac{OB}{OA}=\frac{2}{5}$。
因为$N$为$AF$中点,$AF = 5$,所以$AN=\frac{5}{2}$,
则$BM=\frac{2}{5}×\frac{5}{2}=1$,$AM = AB - BM=5 - 1=4$。
在$Rt\triangle AMN$中,$\tan\angle AMN=\frac{AN}{AM}=\frac{\frac{5}{2}}{4}=\frac{5}{8}$。
$\frac{5}{8}$