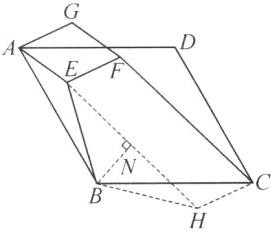
14. (12分)如图,在四边形ABCD中,AD//BC,AE⊥BC于点E,CF⊥AB于点F,AE与CF相交于点G,连接GD,且∠1=∠2,∠3=∠4。
(1)求证:四边形ABCD为平行四边形;
(2)若AG=3,DG=5,求四边形ABCD的面积。

答案:14. (1) 因为$CF⊥ AB$,所以$\angle AFG = 90^{\circ}$.因为$\angle1 = \angle2$,$\angle1 = \angle AGF$,所以$\angle AGF = \angle2$.因为$\angle3 = \angle4$,所以$\angle DCG = \angle AFG = 90^{\circ}$.所以$CF⊥ CD$.所以$AB// DC$.因为$AD// BC$,所以四边形$ABCD$为平行四边形.
(2) 因为$AD// BC$,$AE⊥ BC$,所以$AE⊥ AD$,$\angle AEB = 90^{\circ}$.在$Rt\triangle ADG$中,$AG = 3$,$DG = 5$,由勾股定理,得$AD = \sqrt{DG^{2} - AG^{2}} = 4$.由(1),得四边形$ABCD$为平行四边形,所以$BC = AD = 4$,$AB = DC$.过点$C$作$CH⊥ DG$于点$H$.所以$\angle DHC = 90^{\circ}$,即$\angle AEB = \angle DHC$.因为$\angle3 = \angle4$,所以$\triangle ABE\cong\triangle DCH$(AAS).所以$BE = CH$,$AE = DH$.因为$\angle1 = \angle2$,$CH⊥ DG$,$CE⊥ AE$,所以$CE = CH$.所以$BE = CE$.又$BE + CE = BC$,所以$BE = CE = 2$.又$CG = CG$,所以$Rt\triangle CGE\cong Rt\triangle CGH$(HL).所以$GE = GH$.设$GE = GH = x$,则$DH = DG - GH = 5 - x$,$AE = AG + GE = 3 + x$.所以$5 - x = 3 + x$,解得$x = 1$.所以$AE = 4$.所以四边形$ABCD$的面积为$BC· AE = 4×4 = 16$.
15. (18分)新趋势
综合实践 我们知道,平行四边形的对边平行且相等,利用这一性质,可以为证明线段之间的位置关系和数量关系提供帮助。
(1)如图①,我们在探究三角形中位线DE和第三边BC的关系时,所作的辅助线为“延长DE到点F,使EF=DE,连接CF”,此时DE与DF在同一条直线上,且DE=$\frac{1}{2}$DF。又可证图中的四边形
BCFD
为平行四边形,可得BC与DF的关系是
平行且相等
,于是推导出了“DE//BC,DE=$\frac{1}{2}$BC”;
(2)如图②,四边形ABCD和四边形AEFG都是正方形,△BEH是等腰直角三角形,∠EBH=90°,连接CF,CH。求证:CF=$\sqrt{2}$BE;
(3)如图③,四边形ABCD和四边形AEFG都是菱形,∠ABC=∠AEF=120°,连接BE,CF。直接写出CF与BE之间的数量关系。

答案:15. (1) BCFD 平行且相等 解析:因为$AE = CE$,$DE = EF$,$\angle AED = \angle CEF$,所以$\triangle AED\cong\triangle CEF$(SAS).所以$AD = CF$,$\angle ADE = \angle F$,即$BD// CF$.因为$AD = BD$,所以$BD = CF$.所以四边形BCFD是平行四边形.所以$DF = BC$,$DF// BC$.
(2) 因为四边形$ABCD$是正方形,所以$AB = BC$,$\angle ABC = 90^{\circ}$,即$\angle ABE + \angle CBE = 90^{\circ}$.因为$\triangle BEH$是等腰直角三角形,$\angle EBH = 90^{\circ}$,$BE = BH$,$\angle BEH = \angle BHE = 45^{\circ}$,$\angle CBH + \angle CBE = 90^{\circ}$.所以$\angle ABE = \angle CBH$.所以$\triangle ABE\cong\triangle CBH$(SAS).所以$AE = CH$,$\angle AEB = \angle CHB$.所以$\angle CHE = \angle CHB - \angle BHE = \angle CHB - 45^{\circ} = \angle AEB - 45^{\circ}$.因为四边形$AEFG$是正方形,所以$AE = EF$,$\angle AEF = 90^{\circ}$.所以$EF = CH$.又$\angle AEF + \angle AEB + \angle BEH + \angle FEH = 360^{\circ}$,所以$\angle FEH = 360^{\circ} - \angle AEF - \angle AEB - \angle BEH = 225^{\circ} - \angle AEB$.所以$\angle CHE + \angle FEH = \angle AEB - 45^{\circ} + 225^{\circ} - \angle AEB = 180^{\circ}$.所以$EF// CH$.所以四边形$EFCH$是平行四边形.所以$CF = EH$,即$CF = \sqrt{2}BE$.
(3) $CF = \sqrt{3}BE$. 解析:如图,过点$B$作$BH$,使$\angle EBH = 120^{\circ}$,且$BH = BE$,连接$EH$,$CH$,则$\angle BHE = \angle BEH$.又$\angle BHE + \angle BEH + \angle EBH = 180^{\circ}$,所以$\angle BHE = \angle BEH = 30^{\circ}$.因为$\angle ABC = 120^{\circ}$,所以$\angle ABC = \angle EBH$.所以$\angle ABC - \angle EBC = \angle EBH - \angle EBC$,即$\angle ABE = \angle CBH$.因为四边形$ABCD$和四边形$AEFG$都是菱形,所以$AB = BC$,$AE = EF$.所以$\triangle AEB\cong\triangle CHB$(SAS).所以$AE = CH$,$\angle AEB = \angle CHB$,即$EF = CH$.所以$\angle CHE = \angle CHB - \angle BHE = \angle AEB - 30^{\circ}$.又$\angle AEF = 120^{\circ}$,$\angle AEF + \angle AEB + \angle BEH + \angle FEH = 360^{\circ}$,所以$\angle FEH = 360^{\circ} - \angle AEF - \angle AEB - \angle BEH = 210^{\circ} - \angle AEB$,即$\angle CHE + \angle FEH = 180^{\circ}$.所以$CH// EF$.所以四边形$EFCH$是平行四边形.所以$CF = EH$.过点$B$作$BN⊥ EH$于点$N$,则$BE = 2BN$,$EH = 2EN$.在$Rt\triangle BEN$中,由勾股定理,得$EN = \sqrt{BE^{2} - BN^{2}} = \sqrt{3}BN$.所以$EH = 2\sqrt{3}BN = \sqrt{3}BE$.所以$CF = \sqrt{3}BE$.