11. 已知从边长为$2m + 3$的正方形纸片中剪出一个边长为$m + 3$的正方形之后,剩余部分可剪拼成一个矩形.若拼成的矩形一边长为$m$,则它的另一边长为
$3m + 6$
.
答案:11 $3m + 6$
解析:
原正方形面积为$(2m+3)^2=4m^2 + 12m + 9$,剪出的正方形面积为$(m+3)^2=m^2 + 6m + 9$,剩余部分面积为$4m^2 + 12m + 9 - (m^2 + 6m + 9)=3m^2 + 6m$。因为矩形一边长为$m$,所以另一边长为$(3m^2 + 6m)÷ m=3m + 6$。
$3m + 6$
12. 若$x\neq y$,且$x^{2}-2x + y = m$,$y^{2}-2y + x = m$,则$x + y=$
3
.
答案:12 3
解析:
由题意得:
$\begin{cases}x^2 - 2x + y = m & (1) \\y^2 - 2y + x = m & (2)\end{cases}$
$(1)-(2)$得:$x^2 - 2x + y - (y^2 - 2y + x) = 0$
化简得:$x^2 - y^2 - 3x + 3y = 0$
因式分解:$(x - y)(x + y) - 3(x - y) = 0$
即:$(x - y)(x + y - 3) = 0$
因为$x \neq y$,所以$x - y \neq 0$,则$x + y - 3 = 0$,故$x + y = 3$
3
13. 新趋势
情境素材因式分解:$(3x + y)^{2}-(x + 3y)^{2}$.小明因式分解后,通过代入特殊值检验时,发现左右两边的值不相等,下面是他的解答和检验过程,请认真阅读并完成相应的任务.

任务:
(1)小明的解答是从第几步开始出错的?并帮助他找出错误的原因;
(2)请尝试写出正确的因式分解过程.
答案:13 (1) 第二步开始出错. 原因如下:$y$与$-3y$合并同类项计算错误.
(2) 原式$=(3x + y + x + 3y)(3x + y - x - 3y) = (4x + 4y)(2x - 2y) = 8(x + y)(x - y)$.
14. 计算:$\frac{(
2^{2}-1)×(
3^{2}-1)×···×(202
6^{2}-1)}{1^{2}×2^{2}×3^{2}×···×2026^{2}}=$
$\frac{2027}{4052}$
.
答案:14 $\frac{2027}{4052}$ 解析:原式$=(2 - 1)×(2 + 1)×(3 - 1)×(3 + 1)×···×(2026 - 1)×(2026 + 1)÷(1^2×2^2×3^2×···×2025^2×2026^2) = 1×2×3^2×···×2025^2×2026×2027÷(1^2×2^2×···×2025^2×2026^2) = \frac{2027}{1×2×2026} = \frac{2027}{4052}$
解析:
原式$=\frac{(2-1)(2+1)(3-1)(3+1)···(2026-1)(2026+1)}{1^2×2^2×3^2×···×2026^2}$
$=\frac{1×3×2×4×3×5×···×2025×2027}{(1×2×3×···×2026)^2}$
$=\frac{(1×2×3^2×4^2×···×2025^2×2026)×2027}{(1×2×3×···×2026)^2}$
$=\frac{2027}{1×2×2026}$
$=\frac{2027}{4052}$
15. 新素养
创新意识如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”.
例如:$8 = 3^{2}-1^{2}$,$16 = 5^{2}-3^{2}$,$24 = 7^{2}-5^{2}$,则$8$,$16$,$24$这三个数都是“奇特数”.
(1)$40$
是
“奇特数”,$2020$
不是
“奇特数”(填“是”或“不是”);
(2)设两个连续奇数是$2n - 1$和$2n + 1$(其中$n$取正整数),由这两个连续奇数构造的“奇特数”是$8$的倍数吗?为什么?
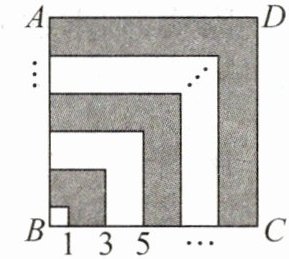
(3)如图,拼叠的正方形边长是从$1$开始的连续奇数,按此规律拼叠到边长为$199$的正方形$ABCD$,求图中阴影部分的面积;
(4)“两个连续偶数的平方差是$8$的倍数.”这个结论正确吗?为什么?
]
答案:15 (1) 是 不是
(2) 是. 理由如下:因为$(2n + 1)^2 - (2n - 1)^2 = (2n + 1 + 2n - 1)×(2n + 1 - 2n + 1) = 8n$, 且$n$为正整数, 所以这两个连续奇数构造的“奇特数”是8的倍数.
(3) 由题意, 得题图中阴影部分的面积为$3^2 - 1^2 + 7^2 - 5^2 + ··· + 199^2 - 197^2 = 8×1 + 8×3 + ··· + 8×99 = 8×(1 + 3 + ··· + 99) = 8×\frac{(1 + 99)×50}{2} = 20000$.
(4) 不正确. 理由如下:设这两个连续偶数分别是$2m, 2m + 2$($m$为正整数), 则$(2m + 2)^2 - (2m)^2 = (2m + 2 + 2m)×(2m + 2 - 2m) = (4m + 2)×2 = 4(2m + 1)$. 因为$m$为正整数, 所以$2m + 1$为奇数, 即$4(2m + 1)$不能被8整除. 所以两个连续偶数的平方差不是8的倍数.