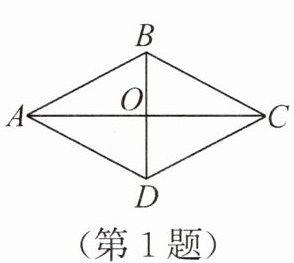
1. (2025·湖南)如图,在四边形 $ABCD$ 中,对角线 $AC$ 与 $BD$ 互相垂直平分,$AB = 3$,则四边形 $ABCD$ 的周长为(
C
)
A.$6$
B.$9$
C.$12$
D.$18$
答案:1.C
解析:
证明:
∵对角线$AC$与$BD$互相垂直平分,
∴四边形$ABCD$是菱形,
∵$AB = 3$,
∴菱形$ABCD$的周长为$4× AB=4×3 = 12$。
C
2. (教材 P81 练习 2 变式)用直尺和圆规作一个以线段 $AB$ 为边的菱形,作图痕迹如图所示,能得到四边形 $ABCD$ 是菱形的依据为(
B
)
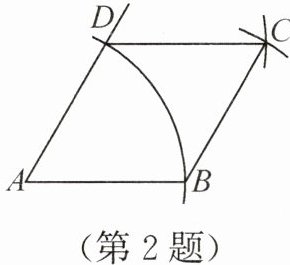
A.一组邻边相等的平行四边形是菱形
B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
答案:2.B
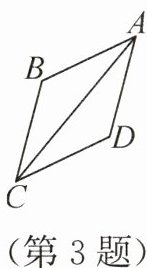
3. 如图,在四边形 $ABCD$ 中,$AC$ 平分 $\angle BAD$,$BC// AD$,$AB// CD$。若 $AD = 6$,则四边形 $ABCD$ 的周长是(
A
)
A.$24$
B.$28$
C.$32$
D.$36$
答案:3.A
解析:
证明:
∵ $BC // AD$,$AB // CD$,
∴ 四边形 $ABCD$ 是平行四边形,
∴ $AD = BC = 6$,$AB = CD$。
∵ $AC$ 平分 $\angle BAD$,
∴ $\angle BAC = \angle DAC$。
∵ $AB // CD$,
∴ $\angle BAC = \angle ACD$,
∴ $\angle DAC = \angle ACD$,
∴ $AD = CD = 6$,
∴ $AB = CD = 6$。
∴ 四边形 $ABCD$ 的周长为 $AB + BC + CD + AD = 6 + 6 + 6 + 6 = 24$。
答案:A
4. 新趋势
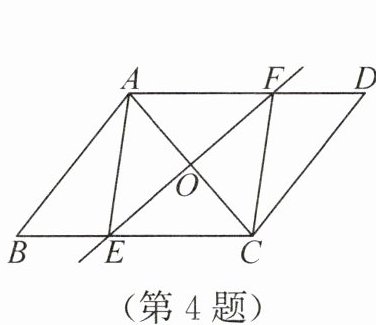
开放探究 如图,在 $□ ABCD$ 中,过 $AC$ 的中点 $O$ 的直线分别交边 $BC$,$AD$ 于 $E$,$F$ 两点,连接 $AE$,$CF$。若添加一个条件使四边形 $AECF$ 是菱形,则这个条件可以是
AE=CE(答案不唯一)
。
答案:4.AE=CE(答案不唯一)
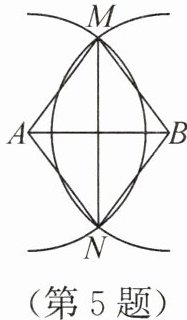
5. (2025·江苏淮安期中)如图,以点 $A$ 为圆心,$5$ 为半径作弧,再以点 $B$ 为圆心,$5$ 为半径作弧,两弧相交于 $M$,$N$ 两点。若 $AB = 6$,则以 $A$,$B$,$M$,$N$ 四点为顶点的四边形的面积是
24
。
答案:5.24
解析:
解:连接 $MN$,交 $AB$ 于点 $O$。
由题意知,$AM = AN = BM = BN = 5$,故四边形 $AMBN$ 为菱形,且 $AB = 6$。
因为菱形的对角线互相垂直平分,所以 $AO = \frac{1}{2}AB = 3$,$MO = NO$,$MN ⊥ AB$。
在 $Rt\triangle AOM$ 中,由勾股定理得:$MO = \sqrt{AM^2 - AO^2} = \sqrt{5^2 - 3^2} = 4$,则 $MN = 2MO = 8$。
四边形 $AMBN$ 的面积为:$\frac{1}{2} × AB × MN = \frac{1}{2} × 6 × 8 = 24$。
24
6. (2025·江苏徐州)如图,在 $□ ABCD$ 中,$E$ 为 $BC$ 的中点,$EF⊥ AC$ 于点 $G$,交 $AD$ 于点 $F$,$AB⊥ AC$,连接 $AE$,$CF$。求证:
(1) $\triangle AGF\cong\triangle CGE$;
(2) 四边形 $AECF$ 是菱形。
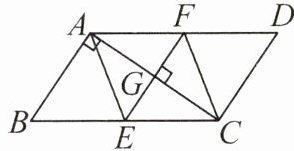
答案:6.(1)因为四边形ABCD是平行四边形,所以AD//BC,即∠CAD = ∠ACB,∠AFG = ∠CEG.又AB⊥AC,所以∠BAC = 90°.又E为BC的中点,所以AE = CE = $\frac{1}{2}$BC.又EF⊥AC,所以AG = CG.所以△AGF≌△CGE(AAS).
(2)由(1),得AG = CG,△AGF≌△CGE,所以GF = GE,即四边形AECF是平行四边形.又AC⊥EF,所以四边形AECF是菱形.
7. 如图,四边形 $ABCD$ 是平行四边形,以点 $A$ 为圆心,$AB$ 的长为半径作弧交 $AD$ 于点 $F$,再分别以 $B$,$F$ 两点为圆心,大于 $\frac{1}{2}BF$ 的长为半径作弧,两弧交于点 $M$,作射线 $AM$ 交 $BC$ 于点 $E$,连接 $BF$,$EF$,则下列结论不一定成立的是(
D
)
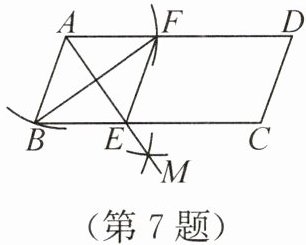
A.$BE = EF$
B.$EF// CD$
C.$AE$ 平分 $\angle BEF$
D.$AB = AE$
答案:7.D
解析:
证明:
∵四边形$ABCD$是平行四边形,
∴$AD// BC$,$AB=CD$,$\angle DAB=\angle BCD$。
由作图知,$AF=AB$,$AM$平分$\angle DAB$,
∴$\angle BAE=\angle FAE$。
∵$AD// BC$,
∴$\angle FAE=\angle AEB$,
∴$\angle BAE=\angle AEB$,
∴$AB=BE$。
∵$AF=AB$,
∴$AF=BE$。
又$AF// BE$,
∴四边形$ABEF$是平行四边形。
∵$AB=BE$,
∴平行四边形$ABEF$是菱形,
∴$BE=EF$(A成立),$AE$平分$\angle BEF$(C成立),$AB// EF$。
∵$AB// CD$,
∴$EF// CD$(B成立)。
无法证明$AB=AE$,
故结论不一定成立的是D。
答案:D
8. 如图,$□ ABCD$ 的面积为 $12$,$AC = BD = 6$,$AC$ 与 $BD$ 交于点 $O$,分别过 $C$,$D$ 两点作 $BD$,$AC$ 的平行线相交于点 $F$,$G$ 是 $CD$ 的中点,$P$ 是四边形 $OCFD$ 边上的动点,连接 $PG$,则 $PG$ 的长的最小值是(
A
)
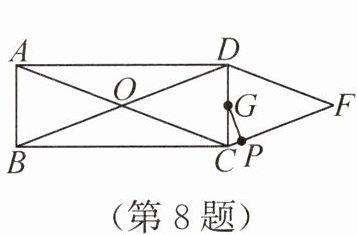
A.$1$
B.$\frac{\sqrt{3}}{2}$
C.$\frac{3}{2}$
D.$3$
答案:8.A
解析:
解:
∵四边形$ABCD$是平行四边形,面积为$12$,$AC=BD=6$,
∴$OA=OC=3$,$OB=OD=3$,且$S_{□ABCD}=4S_{\triangle AOB}=12$,
∴$S_{\triangle AOB}=3$,即$\frac{1}{2}OA· OB·\sin\angle AOB=3$,
代入$OA=OB=3$,得$\sin\angle AOB=\frac{2}{3}$,$\cos\angle AOB=\pm\frac{\sqrt{5}}{3}$(不影响距离计算)。
∵$CF// BD$,$DF// AC$,
∴四边形$OCFD$是平行四边形,且$OC=3$,$OD=3$,$\angle COF=\angle AOB$。
$G$是$CD$中点,$P$是四边形$OCFD$边上动点,$PG$最小值为$G$到边的最短距离。
在$\triangle OCD$中,$OC=OD=3$,$CD$边上的高$h=\sqrt{3^2-(\frac{CD}{2})^2}$,
但$PG$最小值为$G$到$OC$或$OD$的距离。
由面积法,$S_{\triangle OCD}=3$(与$\triangle AOB$等积),$OC=3$,
$G$到$OC$的距离$d=\frac{2S_{\triangle OCD}}{2· OC}=\frac{3}{3}=1$。
故$PG$的最小值是$1$。
答案:A