例1 某中学开展了以“我最支持的戒烟方式”为主题的调查活动。六年级一班同学将调查结果整理分析后,绘制成如下统计图。
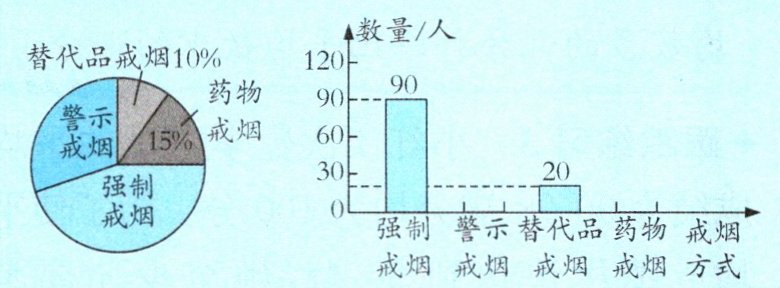
(1)六年级一班同学一共调查了多少人?
(2)支持强制戒烟的占百分之几?支持警示戒烟的占百分之几?
答案:规范解答(1)$20÷10\% = 200$(人)
答:六年级一班同学一共调查了 200 人。
(2)$90÷200 = 45\%$ $1 - 10\% - 15\% -$ $45\% = 30\%$ 答:支持强制戒烟的占 $45\%$,支持警示戒烟的占 $30\%$。
跟踪练习 1 (2025·南通海安市期末)如图是对路人最喜欢喝的饮料进行随机调查后制成的统计图。已知喜欢其他饮料的人数是喜欢奶茶的$\frac{1}{5}$,比喜欢咖啡的少 8 人,请把统计图补充完整。一共调查(
40
)人。

答案:[跟踪练习 1] 25 5 25(由上到下) 40
解析:
奶茶:25%,其他:5%,咖啡:25%,一共调查:40人。
例2 欢欢和乐乐用投掷骰子的方式来决定谁先走棋。乐乐对欢欢说:“若掷到质数,则我先走;若掷到合数,则你先走;若掷到的既不是合数也不是质数,就再来一次。”这样的设计方式公平吗?
答案:规范解答 质数有 2,3,5,合数有 4,6,出现质数的可能性比出现合数的可能性大,这样的设计方式不公平。
跟踪练习 2 (2025·南通海门区期末)把 1~10 这 10 个数分别写在 10 张完全相同的纸条上,做成 10 个纸团,从中任意摸出一个纸团,摸到奇数的可能性比摸到质数的可能性(
)(填“大”或“小”);摸到合数的可能性是$\frac{( )}{( )}$。
答案:[跟踪练习 2] 大$ \frac{1}{2}$