例3(教材P96)
仓库里有以下四种规格的长方形、正方形铁皮。
①长0.6米,宽0.4米;
②长0.6米,宽0.5米;
③长0.5米,宽0.4米;
④边长0.4米。
张师傅想从中选5张铁皮,焊接成一个无盖的长方体(或正方体)水箱,可以选哪几种规格的铁皮,各要选几张?你能找到多少种不同的选法?在下表中填一填。
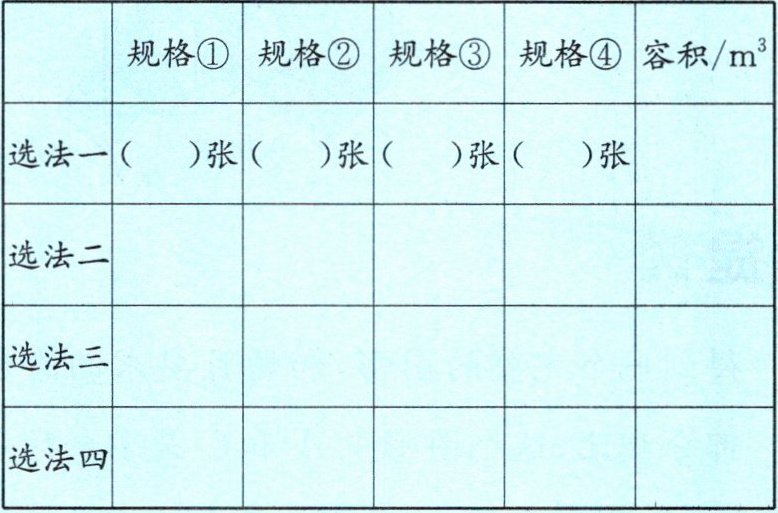
答案:因为题中要求焊接成一个无盖的长方体(或正方体)水箱,所以只要5个面,分别是前、后、左、右和底面。我们可以按顺序先确定底面,即将四种规格的长方形、正方形铁皮依次作为底面,再根据底面的数据确定前、后一组面和左、右一组面。特别要注意的是,正方体是特殊的长方体,也可以焊接成正方体。
规范解答
答案不唯一,如:
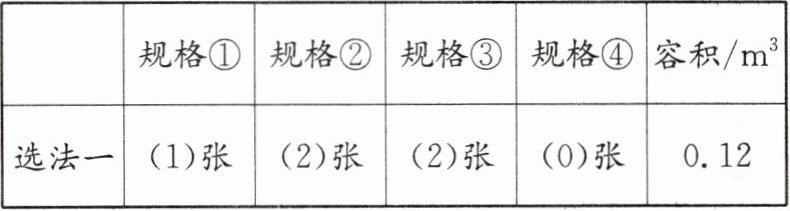
续表
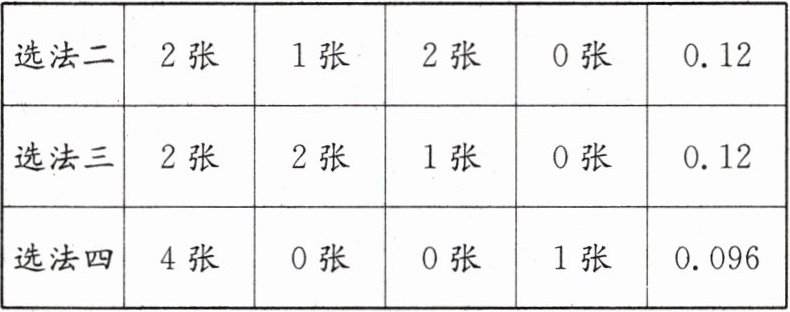
跟踪练习3
仓库里有四种规格的长方形、正方形铁皮(如下图)。王师傅要从中选5张铁皮,焊接成一个无盖的长方体或正方体水箱,要使水箱的容积最大,可以怎样选?容积最大是多少?
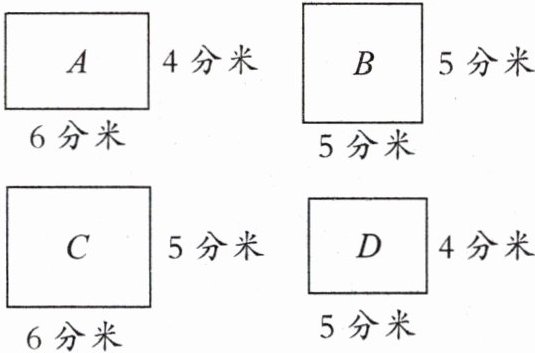
答案:跟踪练习3 选法不唯一,如:选1张B型号铁皮、4张C型号铁皮。 容积最大:5×5×6=150(立方分米) 150立方分米=150升
例4(教材P98)
剪两个同样大的正方形,把其中一个正方形的顶点固定在另一个正方形的中心点上。旋转其中一个正方形,重叠部分的面积有没有变化?你能说明自己的想法吗?
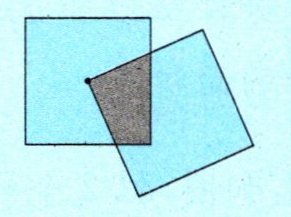
答案:重叠部分是一个不规则的图形,要想办法将它转化为规则的图形。可以连接第一个正方形的两条对角线,如下图。
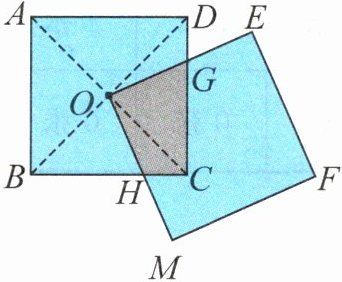
从图中可以看出,三角形 $ ODG $ 和三角形 $ OCH $ 是完全相同的,所以不规则的四边形 $ OGCH $ 的面积可以转化成三角形 $ ODC $ 的面积。因此,无论怎样旋转,重叠部分的面积总是整个正方形面积的 $ \frac{1}{4} $。
规范解答
重叠部分的面积没有变化,总是整个正方形面积的 $ \frac{1}{4} $。