13. 下面是一种利用图形计算整数乘法的方法,根据图中图形表示的规律,可知图⑤所表示的算式为(
21×13=273
),图⑥所表示的算式为(
321×123=39483
)。
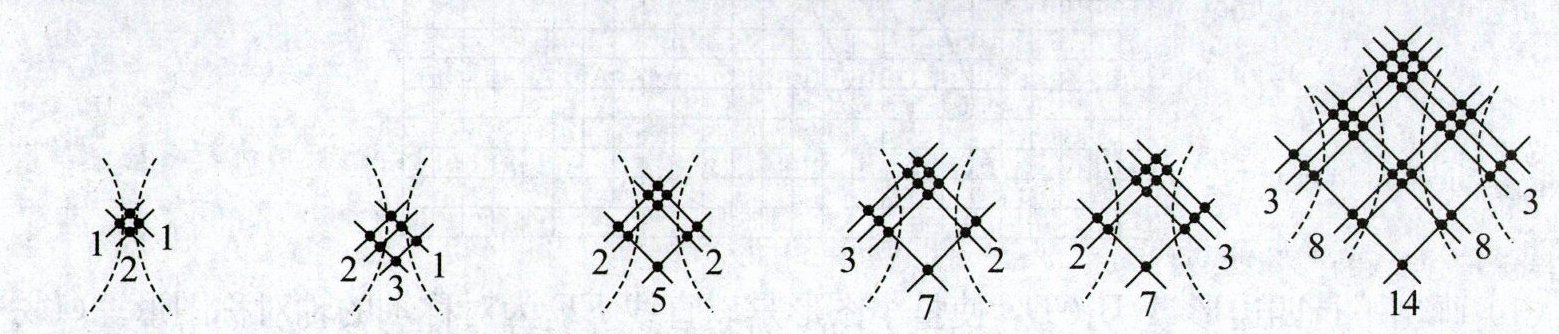
答案:13. 21×13=273 321×123=39483
解析:由题图可知,直线的数量和位置与两个乘数各个数位上的数字有一定关系,从左上角至右下角各组直线的条数依次为第一个乘数由高位到低位上的数字;从左下角至右上角各组直线的条数依次为第二个乘数由高位到低位上的数字。从左往右各区域内的交点个数的和依次为积由高位到低位上的数字。根据以上规律,图⑤所表示的算式为21×13 =273,图⑥所表示的算式为321×123=38(14)83,其中14大于10,要向前一位进1,故前一位上加1,即321×123=3(8 + 1)483,图⑥所表示的算式为321×123=39483。
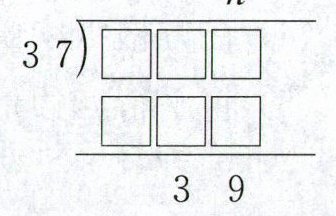
1. 东东计算有余数的除法$\overline{□□□}÷37$时,试商n后,发现余数比除数大了(如图)。这道题正确的商和余数分别是(
D
)。
A.n,2
B.n,36
C.n+1,1
D.n+1,2
答案:1. D
2. 小娟在含盐率20%的盐水中,加入50克盐和200克水,这时盐水的含盐率(
B
)。
A.低于20%
B.等于20%
C.高于20%
D.无法确定
答案:2. B
解析:
加入盐水的含盐率为:$\frac{50}{50 + 200} × 100\% = \frac{50}{250} × 100\% = 20\%$。
因为加入的盐水含盐率等于原盐水含盐率20%,所以混合后盐水的含盐率仍为20%。
B
3. 新素养空
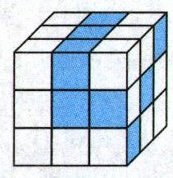
间观念 右图是三个面带有图案的正方体,小明翻动这个正方体,下面(
C
)可能是小明翻动后的样子。

答案:3. C
4. 某羽毛球队中4名队员的身高均在170~185cm。如果一名身高为195cm的队员加入,那么这5名羽毛球队员的平均身高(
C
)。
A.增加7cm
B.最多增加6.25cm
C.增加2~5cm
D.减少5cm
答案:4. C
解析:
设原来4名队员身高总和为$ S $,原来平均身高为$ \overline{x}_1=\frac{S}{4} $,新平均身高为$ \overline{x}_2=\frac{S + 195}{5} $。
身高变化量$ \Delta = \overline{x}_2 - \overline{x}_1 = \frac{S + 195}{5} - \frac{S}{4} = \frac{4(S + 195) - 5S}{20} = \frac{780 - S}{20} $。
因为$ 170 × 4 \leq S \leq 185 × 4 $,即$ 680 \leq S \leq 740 $。
当$ S = 680 $时,$ \Delta = \frac{780 - 680}{20} = 5 \, \mathrm{cm} $;当$ S = 740 $时,$ \Delta = \frac{780 - 740}{20} = 2 \, \mathrm{cm} $。
所以平均身高增加$ 2 ∼ 5 \, \mathrm{cm} $。
C
5. 算盘的一个上珠表示5,一个下珠表示1,用1个上珠和2个下珠一共可以表示(
B
)个不同的三位数。
A.6
B.12
C.15
D.21
答案:5. B
解析:
情况1:上珠在百位
百位:5(1个上珠)
下珠分配:2个下珠可在十位和个位,有3种分法:(2,0)、(1,1)、(0,2)
表示的数:520、511、502(3个)
情况2:上珠在十位
十位:5(1个上珠)
下珠分配:2个下珠可在百位和个位,有3种分法:(2,0)、(1,1)、(0,2)
表示的数:250、151、052(052不是三位数,排除)→ 250、151(2个)
情况3:上珠在个位
个位:5(1个上珠)
下珠分配:2个下珠可在百位和十位,有3种分法:(2,0)、(1,1)、(0,2)
表示的数:205、115、025(025不是三位数,排除)→ 205、115(2个)
情况4:下珠在百位,上珠在十位或个位
百位1个下珠(1),上珠在十位(5),剩余1个下珠在个位:151(重复)
百位1个下珠(1),上珠在个位(5),剩余1个下珠在十位:115(重复)
百位2个下珠(2),上珠在十位(5):250(重复)
百位2个下珠(2),上珠在个位(5):205(重复)
情况5:上珠和下珠在同一数位
百位:5+2=7 → 700(1个)
十位:5+2=7 → 170、270(百位1或2个下珠,2个)
个位:5+2=7 → 107、207(百位1或2个下珠,2个)
总计不同三位数
3+2+2+1+2+2=12(个)
B
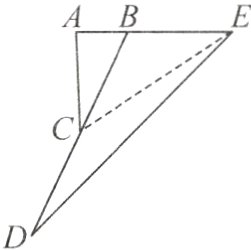
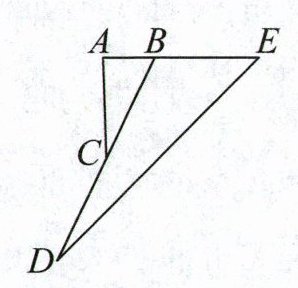
6. 如图,三角形ABC的面积是1平方分米,并且AE:AB=3:1,BD:BC=2:1,那么三角形BDE的面积是(
C
)平方分米。
A.8
B.6
C.4
D.2
答案:6. C 解析:如图,连接CE。因为AE:AB = 3:1,所以BE:AB = 2:1,因为三角形BCE和三角形ABC等高,所以三角形BCE的面积是三角形ABC面积的2倍,即1×2 = 2(平方分米),根据BD:BC = 2:1,且三角形BDE和三角形BCE等高,所以三角形BDE的面积是三角形BCE面积的2倍,即2×2 = 4(平方分米),故选C。