3. 一块长方形菜地,长和宽的比是5:3,长和宽都增加10米,则面积增加1700平方米。这块长方形菜地原来的面积是(
D
)平方米。
A.3350
B.4335
C.5400
D.6000
答案:3.D
解析:
设原来长方形的长为$5x$米,宽为$3x$米。
原来的面积为$5x × 3x = 15x^2$平方米。
长和宽都增加10米后,长为$(5x + 10)$米,宽为$(3x + 10)$米,新面积为$(5x + 10)(3x + 10)$平方米。
根据面积增加1700平方米,可得方程:
$(5x + 10)(3x + 10) - 15x^2 = 1700$
展开左边:
$15x^2 + 50x + 30x + 100 - 15x^2 = 80x + 100$
则:
$80x + 100 = 1700$
解得:
$80x = 1600 \implies x = 20$
原来的长为$5x = 5 × 20 = 100$米,宽为$3x = 3 × 20 = 60$米,原来的面积为$100 × 60 = 6000$平方米。
D
4. 如图,一个圆柱形油桶从车厢的后端滚到前端正好滚了5周。车厢长(
D
)米。

A.3.14
B.6.28
C.6.48
D.6.68
答案:4.D
解析:
解:圆柱形油桶的半径$r = 0.2\space \mathrm{m}$,其周长$C=2\pi r=2×3.14×0.2 = 1.256\space \mathrm{m}$。
滚动5周的距离为$5× C=5×1.256 = 6.28\space \mathrm{m}$。
车厢长度等于滚动距离加上两个半径(油桶从后端滚到前端,起点和终点油桶圆心到车厢两端的距离各为一个半径),即$6.28+2×0.2=6.28 + 0.4=6.68\space \mathrm{m}$。
答案:D
5. (2025·无锡新吴区期末)三角形ABC中,底边BC和它所对应的高都是4厘米。如果把点A和点C同时以2厘米/秒的速度向右平移,就形成一个梯形(如图),经过3秒,形成的梯形面积是(
C
)平方厘米。
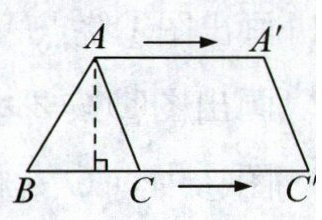
A.64
B.40
C.32
D.20
答案:5.C
解析:
经过3秒,点A和点C向右平移的距离为:$2×3 = 6$厘米。
平移后,梯形的上底为$A'C' = AC$(平移不改变线段长度),下底为$BC' = BC + CC' = 4 + 6 = 10$厘米。
原三角形ABC中,底边BC对应的高为4厘米,即梯形的高为4厘米。
梯形面积公式为:$\frac{(上底 + 下底)×高}{2}$,但此处上底$A'C' = AC$,在原三角形中,$AC$可通过平移分析得,平移后上底实际为$AA' = 6$厘米(此处原解析可能存在图形理解,根据题意形成梯形的上底应为平移距离6厘米,下底为$BC + CC' = 4 + 6 = 10$厘米,高为4厘米)。
代入公式:$\frac{(6 + 10)×4}{2} = \frac{16×4}{2} = 32$平方厘米。
32
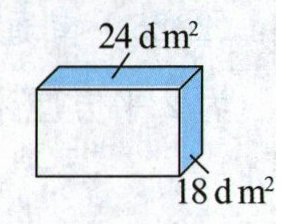
6. 如图,长方体的体积为144立方分米,其中两个面的面积分别为24平方分米和18平方分米,这个长方体的表面积是(
C
)平方分米。
A.90
B.150
C.180
D.200
答案:6.C 解析 根据长方体的体积和上面的面积,可求出长方体的高是144÷24=6(分米);根据长方体的体积和右面的面积,可求出长方体的长是144÷18=8(分米)。根据长方体的长和高,可求出它前面的面积是8×6=48(平方分米)。这个长方体的表面积是(24+18+48)×2=180(平方分米)。
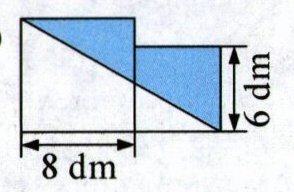
1. 计算图中涂色部分的面积。(4分)
(1)
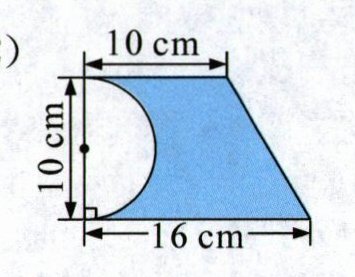
(2)
答案:1.(1)(8+6)×8÷2=56(平方分米$) 8^2 +6^2 -56=44($平方分米) (2)(10+16)×10÷2=130(平方厘米$) 130-3.14×(10÷2)^2 ÷2=90.75($平方厘米)
解析:
(1)$(8+6)×8÷2=56$(平方分米)
$8^{2}+6^{2}-56=44$(平方分米)
(2)$(10+16)×10÷2=130$(平方厘米)
$130-3.14×(10÷2)^{2}÷2=90.75$(平方厘米)
2. 计算下面立体图形的体积。(单位:厘米)(6分)
(1)
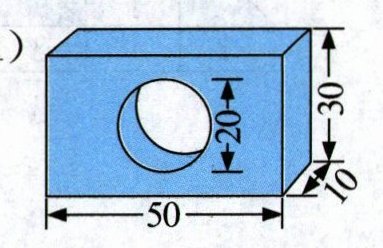
(2)
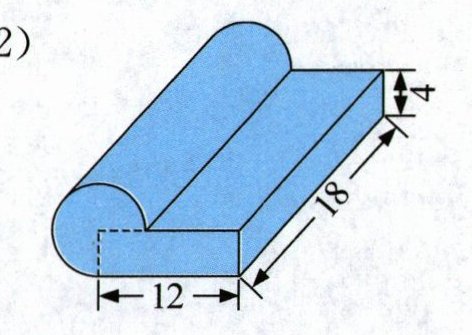
答案:$2.(1)50×10×30-3.14×(20÷2)^2 ×10=11860($立方厘米$) (2)3.14×4^2 ×18×\frac {3}{4}+12×4×18=1542.24($立方厘米)
解析:
(1) $50 × 10 × 30 - 3.14 × (20 ÷ 2)^2 × 10 = 11860$(立方厘米)
(2) $3.14 × 4^2 × 18 × \frac{3}{4} + 12 × 4 × 18 = 1542.24$(立方厘米)