5. 用若干个小正方体搭建一个立体图形,假如从立体图形的右面和上面看到的形状如图①,但从该立体图形的正前方看,可能出现的情况不止一种,例如可能是图②、③的形状。请你仿照②、③的画法在所给的网格图中画出你认为可能的其他 5 种不同结果。
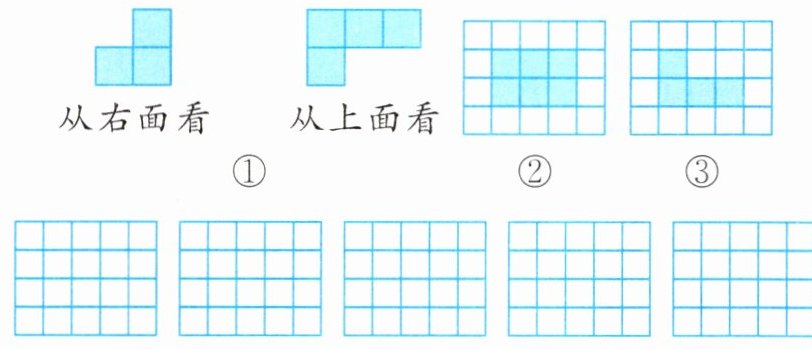
答案:5.

6. 如图①,直角三角形 ABC 中,$AB = 5$ 厘米,$BC = 4$ 厘米,$AC = 3$ 厘米。将三角形 ABC 以点 A 为中心顺时针旋转 $90^{\circ}$ 得到三角形 $AB'C'$。
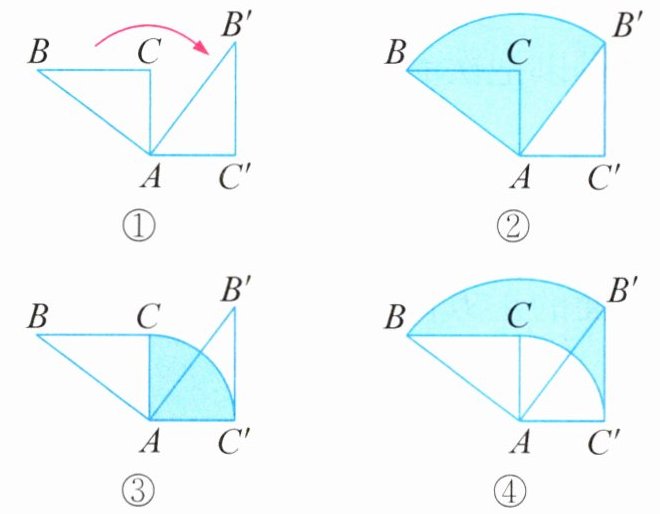
(1)图②的涂色部分是 AB 边在旋转过程中扫过的区域,面积是(
19.625
)平方厘米。
(2)图③的涂色部分是 AC 边在旋转过程中扫过的区域,面积是(
7.065
)平方厘米。
(3)图④的涂色部分是 BC 边在旋转过程中扫过的区域,面积是(
12.56
)平方厘米。
答案:6.(1)19.625 (2)7.065 (3)12.56 解析:(1)AB边在旋转过程中扫过的区域是以AB边为半径的$\frac{1}{4}$圆,那么涂色部分面积为$3.14 × 5^2 × \frac{1}{4} = 19.625$(平方厘米);(2)AC边在旋转过程中扫过的区域是以AC边为半径的$\frac{1}{4}$圆,则涂色部分面积为$3.14 × 3^2 × \frac{1}{4} = 7.065$(平方厘米);(3)涂色部分面积=扇形BAB'的面积+三角形AB'C'的面积-三角形ABC的面积-扇形CAC'的面积,因为三角形AB'C'的面积与三角形ABC的面积相等,所以涂色部分的面积=扇形BAB'的面积-扇形CAC'的面积$= 19.625 - 7.065 = 12.56$(平方厘米)。
解析:
(1)以$AB$为半径的$\frac{1}{4}$圆面积:$3.14×5^{2}×\frac{1}{4}=3.14×25×\frac{1}{4}=78.5×\frac{1}{4}=19.625$平方厘米。
(2)以$AC$为半径的$\frac{1}{4}$圆面积:$3.14×3^{2}×\frac{1}{4}=3.14×9×\frac{1}{4}=28.26×\frac{1}{4}=7.065$平方厘米。
(3)扇形$BAB'$面积减扇形$CAC'$面积:$19.625 - 7.065=12.56$平方厘米。
7. 公元 4 世纪,古希腊数学家佩波斯提出猜想:截面呈正六边形的密铺(不留空隙,也不相互重叠)的蜂窝巢房,是蜜蜂采用最少量的蜂蜡建成的。这一猜想被称为“蜂窝猜想”。
(1)假设蜜蜂用正五边形建蜂巢,结果会怎样?请通过计算说明。
(2)在同种正多边形中,能密铺的只有(
正三角形
),正方形,正六边形。
(3)如下图,图示一中的三种图形面积相等。假设蜜蜂用这三种图形建蜂巢(如图示二),其中正三角形、正六边形图上所标数据为保留两位小数后的结果。(单位:厘米)
图示一:
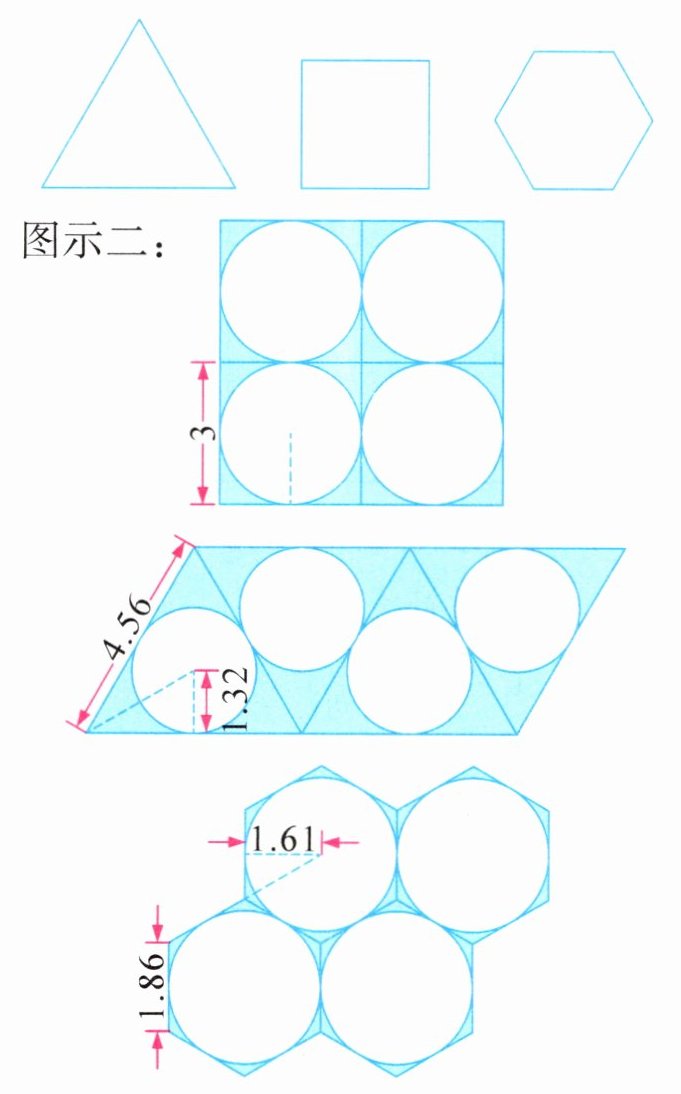
图示二:
那么在建蜂巢的这三种图形中,正方形中的空白圆的直径是(
3
)厘米;正六边形的面积是(
9
)平方厘米;(
正三角
)形的周长最长;(
正六边
)形中的空白圆的面积最大。
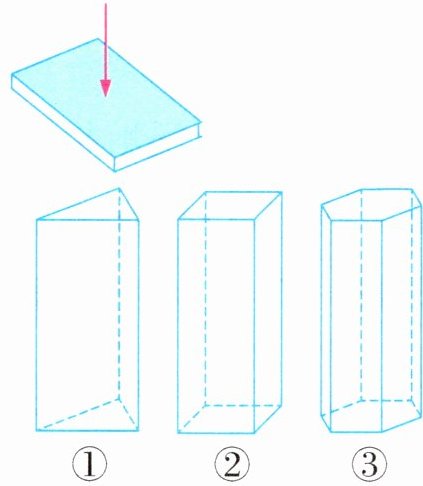
(4)用 3 张同规格的 A4 纸分别折成如下图的三种底面为正多边形的立体图形,比较它们的抗压能力,(
③
)的抗压能力最强。(填序号)
(5)生活中具有蜂巢结构的物体还有蜂窝板材、蜂窝填充料、蜂窝底的锅、移动通信基站的蜂窝状排列等。这种设计有什么好处?
答案:7.(1)正五边形内角和是540°,每一个内角为$540° ÷ 5 = 108°$,$108° × 3 = 324°$,$324° < 360°$。采用正五边形建蜂巢中间有空隙,意味着耗费蜂蜡比较多。(2)正三角形 (3)3 9 正三角 正六边 (4)③ (5)正六边形排列没有空隙,有效空间大,所用材料少,承受力强,构造精巧。(合理即可)
解析:
(1)正五边形内角和是$(5-2)×180^{\circ}=540^{\circ}$,每一个内角为$540^{\circ}÷5 = 108^{\circ}$,$360^{\circ}÷108^{\circ}\approx3.33$,不是整数,所以正五边形不能密铺,会有空隙。
(2)正三角形
(3)3;9;正三角;正六边
(4)③
(5)节省材料、空间利用率高、结构稳定、抗压能力强。