1. (1)把一个长 8 厘米、宽 5 厘米、高 3 厘米的长方体切成两个小长方体,表面积比原来最多增加(
80
)平方厘米,最少增加(
30
)平方厘米。
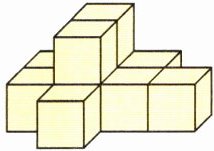
(2)如图,用 10 个体积为 1 立方厘米的小正方体拼搭成一个立体图形,它的表面积是(
36
)平方厘米。如果要把它拼成一个长方体,那么至少需要添加(
14
)个这样的小正方体。
(3)亮点原创·如左下图,一块底面直径是 20 厘米的圆柱形木头,沿底面虚线处竖直切开,正好切成一个最大的正方体,这个正方体的表面积是(
1200
)平方厘米。
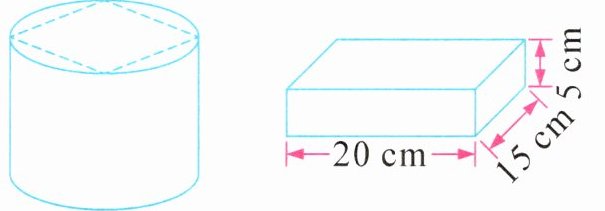
(4)将两个如右上图的糖果盒包在一起,最少需要包装纸(
1300
)平方厘米。
答案:1.(1)80 30 (2)36 14 (3)1200 (4)1300
2. 选一选。
(1)一个长方体与一个圆锥的底面积和体积分别相等,若它们的高之和是 12 厘米,则圆锥的高是(
C
)厘米。
A. 6
B. 4
C. 9
D. 3
(2)一个底面半径是 20 cm,高是 15 cm 的圆柱形铁块,可以熔铸成(
C
)个底面半径是 10 cm,高是 15 cm 的圆锥形铁块。(损耗不计)
A. 3
B. 6
C. 12
D. 24
答案:2.(1)C (2)C
3. 在一个正方体的纸盒中,恰好能放入一个体积为 6.28 立方厘米的圆锥,这个纸盒的容积是(
24
)立方厘米。
答案:3.24
解析:
设正方体的棱长为$a$厘米。
圆锥体积公式为$V = \frac{1}{3}\pi r^2h$,由题意知圆锥底面直径和高都等于正方体棱长$a$,即$r = \frac{a}{2}$,$h = a$。
圆锥体积$V = \frac{1}{3}\pi (\frac{a}{2})^2a = \frac{1}{3}\pi · \frac{a^2}{4} · a = \frac{\pi a^3}{12}$。
已知圆锥体积为$6.28$立方厘米,$\pi$取$3.14$,则$\frac{3.14 a^3}{12} = 6.28$,解得$a^3 = 24$。
正方体容积为$a^3 = 24$立方厘米。
24
4. 如图,一个下面是圆柱、上面是圆锥的容器,圆柱的高是 10 厘米,圆锥的高是 6 厘米,容器内的液面高度是 7 厘米。当把这个容器倒过来放时,从圆锥的顶点到液面的距离是多少厘米?
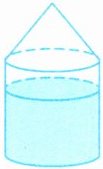
答案:$4.7-6×\frac{1}{3}=5($厘米) 5+6=11(厘米)
解析:
$6×\frac{1}{3}=2$(厘米)
$7-2=5$(厘米)
$5+6=11$(厘米)
答:从圆锥的顶点到液面的距离是11厘米。
5. 新素养
空间观念 图①是一个边长为 60 厘米的正方形纸板,剪掉涂色部分后将其折叠成如图②的长方体盒子,已知该长方体的宽是高的 2 倍,则它的体积是(
8000
)立方厘米。
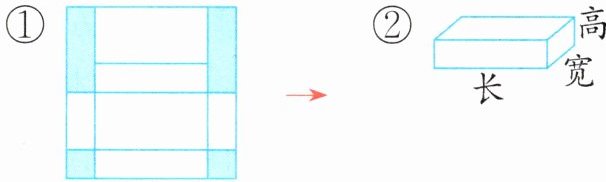
答案:5.8000 解析·由题图可知,正方形边长60厘米包括2条宽和2条高,宽又是高的2倍,可求出高的长度是60÷(1+1+2+2)=10(厘米),则宽是10×2=20(厘米),长是60-10×2=40(厘米),所以长方体盒子的体积是40×20×10=8000(立方厘米)。
解析:
设长方体的高为$h$厘米,因为宽是高的2倍,所以宽为$2h$厘米。
由图①可知,正方形边长60厘米等于2条高加2条宽,即$2h + 2×2h=60$,
$2h + 4h=60$,
$6h=60$,
$h=10$。
则宽为$2h = 2×10=20$厘米,长为$60 - 2h=60 - 2×10=40$厘米。
体积为长×宽×高,即$40×20×10 = 8000$立方厘米。
8000
6. (2025·盐城亭湖区期末)一个长方体容器,底面是一个边长为 60 厘米的正方形,容器里直立着一个高 1 米、底面是边长为 15 厘米的正方形的长方体铁块,这时容器里的水深 0.5 米。现在把铁块轻轻地向上提起 24 厘米,那么露出水面的铁块上被水浸湿的部分长多少厘米?
答案:6.0.5米=50厘米 (60×60-15×15)×50=168750(立方厘米) 60×60×24=86400(立方厘米) (168750-86400)÷(60×60-15×15)=24.4(厘米) 50-24.4=25.6(厘米)