1. $0.73m = ( )\_\_\_\_\_$)dm$ $8m^{2} = ( )______$)dm^{2}$ $70$公顷$ = ( )$_________$$)km^{2} = ( )______$)m^{2}$
答案:1. 7.3 800 0.7 700000
解析:
7.3 dm;800 dm²;0.7 km²;700000 m²
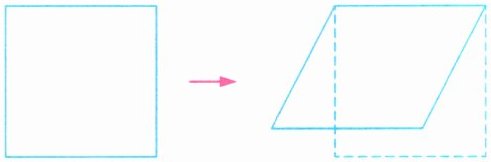
2. (1) 如图,用一根 $32$ 厘米长的铁丝先围成一个正方形框架,再把它拉成一个平行四边形,面积减少了 $12$ 平方厘米,拉成的平行四边形的高是(
6.5
)
厘米
$)$厘米。
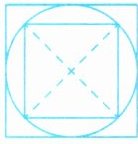
(2) (2025·蚌埠淮上区期末) 半径 $20$ 厘米的圆的外面和里面各有一个正方形(如图)。外面正方形的面积是(
1600
)
平方厘米
$)$平方厘米。里面正方形的面积是(
800
)
平方厘米
$)$平方厘米。
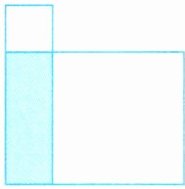
(3) 如图,涂色部分是一个长方形,周长是 $30$ 厘米。若分别以它的长和宽为边长画出 $2$ 个正方形,正方形的面积和是 $137$ 平方厘米,则涂色部分的面积是(
44
)
平方厘米
$)$平方厘米。
答案:2. (1) 6.5 (2) 1600 800 (3) 44
解析:
(1) 正方形边长:$32÷4 = 8$厘米,正方形面积:$8×8 = 64$平方厘米,平行四边形面积:$64 - 12 = 52$平方厘米,平行四边形高:$52÷8 = 6.5$厘米。
(2) 外面正方形边长:$20×2 = 40$厘米,面积:$40×40 = 1600$平方厘米;里面正方形对角线长:$20×2 = 40$厘米,面积:$\frac{40×40}{2} = 800$平方厘米。
(3) 长方形长+宽:$30÷2 = 15$厘米,$(长+宽)^2 = 15^2 = 225$平方厘米,$长^2 + 宽^2 = 137$平方厘米,$2×长×宽 = 225 - 137 = 88$,长方形面积:$88÷2 = 44$平方厘米。
(1) 6.5
(2) 1600;800
(3) 44
3. 计算下面各图中涂色部分的面积。

答案:3. 4×4+(7-4)×15=61(dm²)
$3. 14×(6÷2)²-6×6×\frac{1}{2}=10.26(cm²)$
4. 如图,四边形 $ABCD$ 是平行四边形,$BE:EC = 1:2$,$F$ 是 $DC$ 的中点,三角形 $ABE$ 的面积是 $12$ 平方厘米,那么三角形 $ADF$ 的面积是(
B
)
$)$平方厘米。
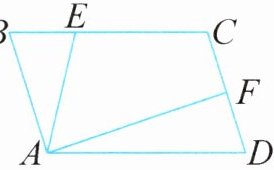
A.$12$
B.$18$
C.$24$
D.$30$
答案:4. B
解析:
证明:设平行四边形$ABCD$的底$BC$为$b$,高为$h$,则其面积为$S = bh$。
因为$BE:EC = 1:2$,所以$BE=\frac{1}{3}BC=\frac{1}{3}b$。
三角形$ABE$以$BE$为底,高与平行四边形相同为$h$,其面积$S_{\triangle ABE}=\frac{1}{2}× BE× h=\frac{1}{2}×\frac{1}{3}b× h=\frac{1}{6}bh = 12$,故$bh=72$。
$F$是$DC$中点,$DC = AB = b$,则$DF=\frac{1}{2}DC=\frac{1}{2}b$。
三角形$ADF$以$DF$为底,高为$h$,面积$S_{\triangle ADF}=\frac{1}{2}× DF× h=\frac{1}{2}×\frac{1}{2}b× h=\frac{1}{4}bh=\frac{1}{4}×72 = 18$。
答案:B
5. 如图,直角三角形 $ABC$ 中的空白部分是正方形,且正方形的一个顶点 $D$ 在直角三角形的斜边上。已知涂色部分的面积和是 $6$ 平方厘米,求线段 $BD$ 的长。
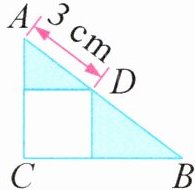
答案:5. 6×2÷3=4(厘米)
6. 如图,将一个三角形沿虚线折叠后得到一个多边形,这个多边形的面积是原三角形面积的$\frac{5}{8}$。若多边形中涂色部分的面积为 $8$ 平方厘米,则原三角形的面积是(
32
)
平方厘米
$)$平方厘米。
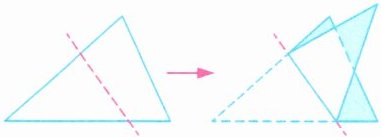
答案:6. 32 解析 原三角形的面积比多边形的面积多的部分是其中的空白四边形的面积,因此空白四边形的面积是原三角形面积的$ 1-\frac{5}{8}=\frac{3}{8},$所以涂色部分的面积是原三角形面积的$ \frac{5}{8}-\frac{3}{8}=\frac{1}{4},$再用$ 8÷\frac{1}{4} $求出原三角形的面积。
解析:
设原三角形面积为$S$平方厘米。
折叠后多边形面积为原三角形面积的$\frac{5}{8}$,则空白四边形面积为$S - \frac{5}{8}S=\frac{3}{8}S$。
涂色部分面积 = 多边形面积 - 空白四边形面积,即$\frac{5}{8}S - \frac{3}{8}S=\frac{2}{8}S=\frac{1}{4}S$。
已知涂色部分面积为$8$平方厘米,可得$\frac{1}{4}S = 8$,解得$S=8÷\frac{1}{4}=32$。
32
7. 亮点原创·如图,圆的面积为 $7.065$ 平方厘米,半圆形的面积为 $25.12$ 平方厘米,求涂色部分的面积。
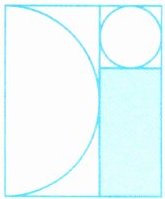
答案:7. 25.12×2=50.24(平方厘米)
50.24÷3.14=16 16=4×4
7.065÷3.14=2.25 2.25=1.5×1.5
(4×2-1.5×2)×(1.5×2)=15(平方厘米)
解析 已知半圆形的面积为 25.12 平方厘米,求出半圆形的半径为 4 厘米,直径为 8 厘米。已知圆的面积是 7.065 平方厘米,求出圆的半径为 1.5 厘米,直径为 3 厘米。因此涂色部分的面积为(8-3)×3=15(平方厘米)。