1. 一个圆按 $4:1$ 的比放大后,大圆的半径和小圆的半径的比是(
4:1
),周长比是(
4:1
),面积比是(
16:1
)。如果把一个圆按 $n:1$ 的比放大,放大后与放大前的图形对应的半径比是(
n:1
),周长比是(
n:1
),面积比是(
$n^2$:1
)。
答案:1. 4:1 4:1 16:1 n:1 n:1 $n^2$:1
解析:
4:1;4:1;16:1;n:1;n:1;$n^2$:1
2. 一个等边三角形放大后的面积是原来的 $16$ 倍,高一定是原来的(
4
)倍。
答案:2. 4
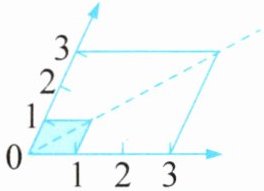
3. (2025·泰州兴化市期末)下图中有两个平行四边形,把其中的小平行四边形按(
3
):$1$ 的比放大可以得到大平行四边形。如果小平行四边形的面积是 $10$ 平方厘米,那么空白部分的面积是(
80
)平方厘米。
答案:3. 3 80
4. (1)把一个长方形按 $5:1$ 的比放大,放大后长方形的面积是 $50\mathrm{cm}^2$,则原长方形的面积是(
B
)$\mathrm{cm}^2$。
A. $10$
B. $2$
C. $250$
(2)把一个正方体按 $1:2$ 的比缩小,缩小后正方体的底面积是原来正方体底面积的(
B
),缩小后正方体的体积是原来正方体体积的(
C
)。
A. $\frac{1}{2}$
B. $\frac{1}{4}$
C. $\frac{1}{8}$
D. $\frac{1}{16}$
答案:4. (1) B (2) B C
5. 新情境 人文历史 北京故宫是中国现存规模最大、保存最完整的古建筑群,占地呈长方形。在比例尺是 $1:6000$ 的图上量得故宫长 $16$ 厘米,宽 $12.5$ 厘米。北京故宫的实际占地面积是多少平方米?
答案:5. 16×6000=96000(厘米) 96000厘米=960米 12.5×6000=75000(厘米) 75000厘米=750米 960×750=720000(平方米)
6. 一个体积是 $50$ 立方厘米的长方体按 $2:1$ 的比放大后,体积是(
400
)立方厘米。
答案:6. 400
解析:
长方体按$2:1$放大,长、宽、高均变为原来的$2$倍。设原长方体长、宽、高分别为$a$、$b$、$c$,原体积$V = abc = 50$立方厘米。放大后长、宽、高分别为$2a$、$2b$、$2c$,放大后体积$V' = 2a×2b×2c = 8abc = 8V$。则放大后体积为$8×50 = 400$立方厘米。
400
7. 若把一个直角三角形的直角边按 $1:4$ 的比缩小,你能说一说他们三人谁对谁错吗?并说明理由。
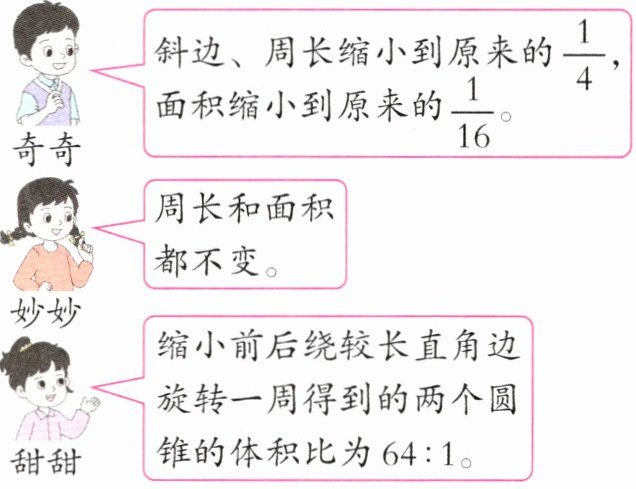
答案:7. 奇奇和甜甜说的是对的,妙妙说的是错的。理由如下:一个直角三角形的直角边按1:4的比缩小后,斜边和周长都缩小到原来的$\frac{1}{4}$,根据三角形面积计算公式“$S=ah ÷ 2$”可知,面积缩小到原来的$\frac{1}{16}$。假定缩小前的两条直角边分别为8、4。缩小前的体积:$4^2 \pi×8×\frac{1}{3}= \frac{128\pi}{3}$,缩小后的体积:$1^2 \pi×2×\frac{1}{3}=\frac{2\pi}{3}$,$\frac{128\pi}{3}:\frac{2\pi}{3}=64:1$。
解析:
奇奇和甜甜说的是对的,妙妙说的是错的。理由如下:一个直角三角形的直角边按$1:4$的比缩小后,斜边和周长都缩小到原来的$\frac{1}{4}$,根据三角形面积计算公式$S=\frac{1}{2}ah$可知,面积缩小到原来的$(\frac{1}{4})^2 = \frac{1}{16}$。假定缩小前的两条直角边分别为$8$、$4$($8$为较长直角边),缩小后的直角边分别为$2$、$1$($2$为较长直角边)。缩小前绕较长直角边旋转一周得到的圆锥体积:$\frac{1}{3}\pi×4^2×8 = \frac{128\pi}{3}$,缩小后绕较长直角边旋转一周得到的圆锥体积:$\frac{1}{3}\pi×1^2×2 = \frac{2\pi}{3}$,体积比为$\frac{128\pi}{3}:\frac{2\pi}{3}=64:1$。
8. 新素养
几何直观 将一个圆柱的底面半径和高都缩小为原来的 $\frac{1}{2}$,缩小后与缩小前圆柱的侧面积之比是(
1:4
)。
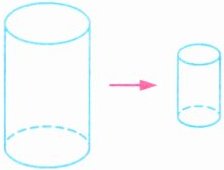
答案:8. 1:4 解析 圆柱的侧面积=底面周长×高,底面半径缩小为原来的$\frac{1}{2}$,那么底面周长也缩小为原来的$\frac{1}{2}$,高缩小为原来的$\frac{1}{2}$,因此缩小后与缩小前圆柱的侧面积之比是1:4。
解析:
圆柱的侧面积公式为$S = 2\pi rh$。
设原来圆柱的底面半径为$r$,高为$h$,则原来的侧面积$S_1=2\pi rh$。
缩小后圆柱的底面半径为$\frac{1}{2}r$,高为$\frac{1}{2}h$,缩小后的侧面积$S_2 = 2\pi×(\frac{1}{2}r)×(\frac{1}{2}h)=\frac{1}{2}\pi rh$。
所以缩小后与缩小前圆柱的侧面积之比为$S_2:S_1=\frac{1}{2}\pi rh:2\pi rh = 1:4$。
1:4
9. 将一个小圆放大成一个大圆,它们的面积之差是 $209$ 平方厘米,小圆与大圆的直径比是 $9:10$,小圆的面积是多少平方厘米?
答案:9. $9^2:10^2=81:100$ 209÷(100-81)=11(平方厘米) 11×81=891(平方厘米) 解析 小圆与大圆直径比为9:10,则面积比就是$9^2:10^2=81:100$,面积之差是209平方厘米,正好就对应增加的份数:100-81=19(份),1份的面积是209÷19=11(平方厘米),小圆的面积是81份,即11×81=891(平方厘米)。
解析:
小圆与大圆的直径比是$9:10$,则面积比是$9^{2}:10^{2}=81:100$。
面积差对应的份数为$100 - 81=19$份。
每份面积为$209÷19 = 11$平方厘米。
小圆面积为$11×81 = 891$平方厘米。
答:小圆的面积是$891$平方厘米。