1. 根据比例的基本性质,在括号里填合适的数。
$ \frac{1}{3}:\frac{1}{10}=\frac{7}{9}:(\quad) $
$ \frac{1.2}{0.15}=\frac{1.6}{(\quad)} $
$ (\quad):6=0.15:1.8 $
$ 0.6:0.36=\frac{5}{6}:(\quad) $
答案:1. $\frac{7}{30}$ 0.2 0.5 0.5
2. 用 $ x $,2,6 和 12 这四个数组成比例,$ x $ 最小是($\quad$),写出这个比例:($\quad$);$ x $ 最大是($\quad$),写出这个比例:($\quad$)。
答案:2. 1 2:1=12:6(答案不唯一) 36 6:2=36:12(答案不唯一)
3. 在一个比例中,两个外项都是质数,它们的积是 22,一个内项是这个积的 $ \frac{1}{10} $,另一个内项是($\quad$)。
答案:3. 10
解析:
22的因数中质数为2和11,所以两个外项为2和11。一个内项为$22×\frac{1}{10}=\frac{11}{5}$。设另一个内项为$x$,根据比例的基本性质可得$2×11=\frac{11}{5}x$,解得$x=10$。
10
4. (2025·扬州江都区期末)新情境 真实生活姐姐按照蜂蜜与水的质量比是 $ 1:20 $ 调制了一杯蜂蜜水,调匀后喝了一半,然后又加入 120 克水,要使蜂蜜水口感不变,姐姐需要加入蜂蜜($\quad$)克。
答案:4. 6
解析:
设姐姐原来调制的蜂蜜水总质量为$x$克,其中蜂蜜质量为$\frac{1}{1 + 20}x=\frac{1}{21}x$克,水的质量为$\frac{20}{21}x$克。
喝了一半后,剩余蜂蜜水质量为$\frac{x}{2}$克,剩余蜂蜜质量为$\frac{1}{2} × \frac{1}{21}x=\frac{1}{42}x$克,剩余水的质量为$\frac{1}{2} × \frac{20}{21}x=\frac{10}{21}x$克。
加入120克水后,水的总质量变为$\frac{10}{21}x + 120$克,设需加入蜂蜜$y$克,此时蜂蜜总质量为$\frac{1}{42}x + y$克。
要使口感不变,蜂蜜与水的质量比仍为$1:20$,则$(\frac{1}{42}x + y):(\frac{10}{21}x + 120)=1:20$。
由比例性质可得:$20(\frac{1}{42}x + y)=\frac{10}{21}x + 120$,化简得$\frac{10}{21}x + 20y=\frac{10}{21}x + 120$,解得$20y = 120$,$y = 6$。
6
5. 解比例。
$ \frac{5}{4}:\frac{5}{8}=24:x $
$ \frac{75}{1.2}=\frac{25}{x} $
$ x:3.2=1.5:16 $
$ \frac{1}{8}:\frac{1}{10}=\frac{1}{4}:x $
答案:5. $x=12$ $x=0.4$ $x=0.3$ $x=\frac{1}{5}$
解析:
$\frac{5}{4}:\frac{5}{8}=24:x$
解:$\frac{5}{4}x=\frac{5}{8}×24$
$\frac{5}{4}x=15$
$x=15×\frac{4}{5}$
$x=12$
$\frac{75}{1.2}=\frac{25}{x}$
解:$75x=1.2×25$
$75x=30$
$x=30÷75$
$x=0.4$
$x:3.2=1.5:16$
解:$16x=3.2×1.5$
$16x=4.8$
$x=4.8÷16$
$x=0.3$
$\frac{1}{8}:\frac{1}{10}=\frac{1}{4}:x$
解:$\frac{1}{8}x=\frac{1}{10}×\frac{1}{4}$
$\frac{1}{8}x=\frac{1}{40}$
$x=\frac{1}{40}×8$
$x=\frac{1}{5}$
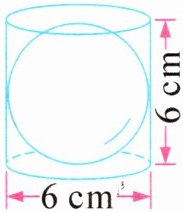
6. 如图是一个“圆柱容球”模型,已知球与圆柱的体积之比是 $ 2:3 $,那么这个球的体积是($\quad$)立方厘米。
A.$ 36π $
B.$ 54π $
C.$ 81π $
D.$ 128π $
答案:6. A
解析:
圆柱底面半径 $ r = \frac{6}{2} = 3 \, \mathrm{cm} $,高 $ h = 6 \, \mathrm{cm} $。
圆柱体积 $ V_{\mathrm{圆柱}} = \pi r^2 h = \pi × 3^2 × 6 = 54\pi \, \mathrm{cm}^3 $。
由球与圆柱体积比 $ 2:3 $,设球体积为 $ V_{\mathrm{球}} $,则 $ \frac{V_{\mathrm{球}}}{54\pi} = \frac{2}{3} $。
解得 $ V_{\mathrm{球}} = 54\pi × \frac{2}{3} = 36\pi \, \mathrm{cm}^3 $。
A
7. 亮点原创·如图,把左边的梯形按一定的比放大后得到右边的梯形,求未知数 $ x $ 和 $ y $。(单位:cm)
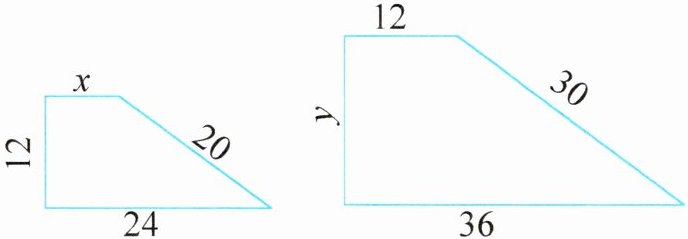
答案:7. $x:12=24:36$ $x=8$
$12:y=20:30$ $y=18$
8. 如图,一个大长方形被分成四个小长方形,其中三个小长方形的面积分别是 8 平方厘米、6 平方厘米和 5 平方厘米,涂色部分的面积是($\quad$)平方厘米。
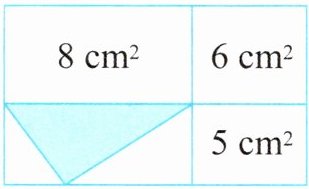
答案:8. $\frac{10}{3}$ 解析 设涂色部分所在小长方形的面积为$x$平方厘米,$x:5=8:6$,求出$x=\frac{20}{3}$,则涂色部分的面积是$\frac{20}{3} × \frac{1}{2} = \frac{10}{3}$(平方厘米)。
解析:
设涂色部分所在小长方形的面积为$x$平方厘米,由比例关系可得$x:5 = 8:6$,解得$x=\frac{20}{3}$,则涂色部分面积为$\frac{20}{3}×\frac{1}{2}=\frac{10}{3}$平方厘米。
$\frac{10}{3}$
9. 某商店一件大衣和一条裤子的价格比为 $ 24:13 $,周年庆时每件商品降价 150 元,此时大衣和裤子的价格比为 $ 21:10 $。降价后的大衣多少元?
答案:9. $150 ÷ (\frac{24}{24-13} - \frac{21}{21-10}) × \frac{21}{21-10}=1050$(元) 解析 由题意可知,大衣和裤子价格的差是不变量,把价格差看作单位“1”,转化为
解析:
设大衣和裤子的价格差为单位“1”。
降价前大衣价格占价格差的比例为:$\frac{24}{24 - 13} = \frac{24}{11}$
降价后大衣价格占价格差的比例为:$\frac{21}{21 - 10} = \frac{21}{11}$
价格差为:$150÷(\frac{24}{11}-\frac{21}{11}) = 150÷\frac{3}{11}=550$(元)
降价后的大衣价格为:$550×\frac{21}{11}=1050$(元)
1050