1. 某人徒步旅行,平路每天走 38 千米,山路每天走 23 千米,他 15 天共走了 450 千米。他一共走了(
184
)千米的山路,走了(
266
)千米的平路。
答案:1. 184 266
解析:
设走平路用了$x$天,走山路用了$y$天。
$\begin{cases}x + y = 15\\38x + 23y = 450\end{cases}$
由$x = 15 - y$代入$38x + 23y = 450$,得$38(15 - y)+23y = 450$
$570 - 38y + 23y = 450$
$-15y = -120$
$y = 8$
山路路程:$23×8 = 184$(千米)
平路路程:$450 - 184 = 266$(千米)
184;266
2. 两根蜡烛,第一根燃去$\frac{3}{5}$,第二根燃去$\frac{5}{7}$,剩下的长度恰好相等。原来两根蜡烛的长度比是(
5 : 7
)。
答案:2. 5 : 7
解析:
设第一根蜡烛原来长度为$a$,第二根蜡烛原来长度为$b$。
第一根燃去$\frac{3}{5}$,剩下长度为$a(1 - \frac{3}{5})=\frac{2}{5}a$;
第二根燃去$\frac{5}{7}$,剩下长度为$b(1 - \frac{5}{7})=\frac{2}{7}b$。
由剩下长度相等,得$\frac{2}{5}a=\frac{2}{7}b$,化简得$\frac{a}{b}=\frac{5}{7}$,即$a:b = 5:7$。
5 : 7
3. 六年级一班原来的男生人数占全班总人数的$\frac{4}{9}$,新学期转进 1 名男生,转走 1 名女生,这时女生人数占全班总人数的$\frac{8}{15}$。六年级一班原来有男生(
20
)名。
答案:3. 20 解析 原来男生人数占全班总人数的$\frac{4}{9}$,新学期转进1名男生,转走1名女生,总人数不变,这时男生人数占全班总人数的$1 - \frac{8}{15} = \frac{7}{15}$,则总人数为$1 ÷ ( \frac{7}{15} - \frac{4}{9} ) = 45$(人),原来男生人数为$45 × \frac{4}{9} = 20$(人)。
解析:
设六年级一班原来全班总人数为$x$人。
原来男生人数为$\frac{4}{9}x$,女生人数为$x - \frac{4}{9}x=\frac{5}{9}x$。
新学期转进1名男生,转走1名女生后,总人数仍为$x$人,此时女生人数为$\frac{5}{9}x - 1$。
由这时女生人数占全班总人数的$\frac{8}{15}$,可得方程:$\frac{5}{9}x - 1 = \frac{8}{15}x$
解方程:
$\frac{5}{9}x - \frac{8}{15}x = 1$
通分:$\frac{25}{45}x - \frac{24}{45}x = 1$
$\frac{1}{45}x = 1$
$x = 45$
原来男生人数为$\frac{4}{9}×45 = 20$(名)
20
1. 新趋势
算理理解 一筐苹果的质量正好是一筐梨的$\frac{2}{3}$,用图表示这个数量关系,正确的是(
C
)。
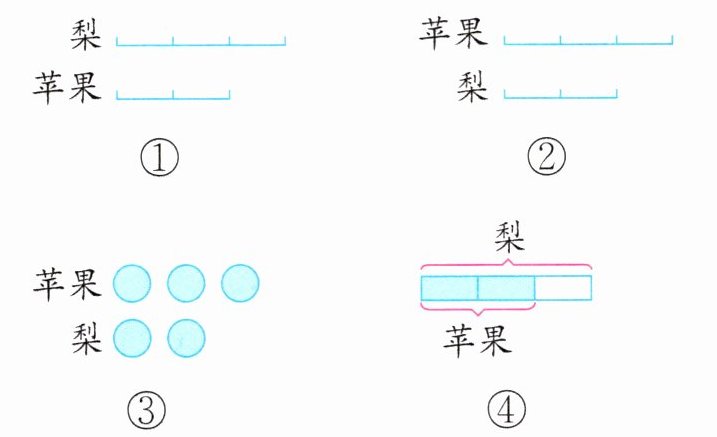
A.①②
B.①③
C.①④
D.①③④
答案:1. C
2. 草地上鸡和兔都抬起一半脚后,地上的脚比头多 5 个,草地上一定有(
A
)。
A.5 只兔
B.5 只鸡
C.10 只兔
D.10 只鸡
答案:2. A 解析 鸡有2只脚,兔有4只脚,都抬起各自的一半脚后,鸡有1只脚,兔有2只脚,鸡的脚与头的数量相等,一只兔的脚比头多1个,而地上的脚比头多5个,说明草地上有5只兔。
1. (2025·淮安市期末)2025 年淮安马拉松参赛规模为 20000 人,马拉松分“全马”“半马”和“健康跑”三种,参加“全马”的有 7000 人,参加“半马”和“健康跑”的人数之比为$6:7$。
(1)参加“半马”的有多少人?
(2)参加“健康跑”的人数占总人数的几分之几?
答案:1. (1)$(20000 - 7000) × \frac{6}{6 + 7} = 6000$(人)
(2)$(20000 - 7000 - 6000) ÷ 20000 = \frac{7}{20}$
2. (2025·无锡新吴区期末改编)明代数学著作《算法统宗》里有一道算题:“一百馒头一百僧,大僧三个更无争。小僧三人分一个,大小和尚得几丁?”译文:100 个和尚吃 100 个馒头。大和尚一人吃 3 个,小和尚 3 人吃一个。大、小和尚各有多少人?
答案:2. 假设全是大和尚,需要馒头:$100 × 3 = 300$(个) 小和尚:$(300 - 100) ÷ ( 3 - \frac{1}{3} ) = 75$(人) 大和尚:$100 - 75 = 25$(人)
解析:
假设全是大和尚,需要馒头:$100×3 = 300$(个)
小和尚:$(300 - 100)÷(3 - \frac{1}{3})=75$(人)
大和尚:$100 - 75 = 25$(人)
答:大和尚有25人,小和尚有75人。
3. 小羽的集邮册里有 5 元、1 元和 8 角的三种邮票共 30 枚,总面值是 60.4 元,其中,5 元和 8 角的邮票枚数相等。三种邮票各有多少枚?
答案:3. 8角$= 0.8$元 $(5 + 0.8 × 30 - 60.4) ÷ ( 2.9 - 1 ) = 14$(枚)
5元和8角各有:$(30 - 14) ÷ 2 = 8$(枚)
解析 由于5元和8角的邮票枚数相等,因此假设30枚邮票全是$(5 + 0.8) ÷ 2 = 2.9$(元)的,则总面值为$2.9 × 30 = 87$(元),比实际面值多了$87 - 60.4 = 26.6$(元)。多出的26.6元是因为把1元的当成了2.9元的,所以可以求出1元的邮票有$26.6 ÷ ( 2.9 - 1 ) = 14$(枚),进而求出5元和8角的邮票各有多少枚。