1. 动物园里鸵鸟和长颈鹿共有15只,它们共有38条腿。鸵鸟和长颈鹿各有多少只?
(1) 按照下面的步骤画图。
① 画15个“○”,表示一共有15只动物。假设15只动物全是鸵鸟,给每只动物画上2条腿。
② 算一算,画出的腿比38条腿少(
8
)条。
③ 1只鸵鸟比1只长颈鹿少2条腿,给其中(
4
)只动物再各添上2条腿,就可以使画出的腿正好是38条。
④ 此时鸵鸟有(
11
)只,长颈鹿有(
4
)只。
(2) 先假设鸵鸟和长颈鹿的只数如下表,再调整。
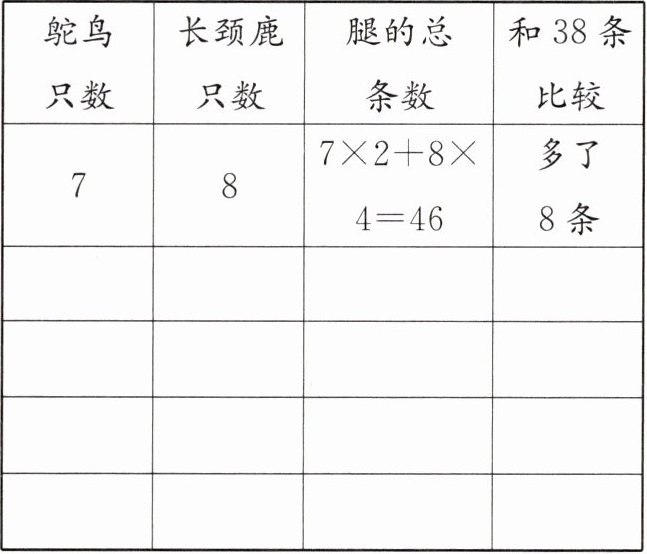
答案:1 (1) ①

② 8 ③ 4 ④ 11 4
(2)

2. 有一首民谣:“一队猎手一队狗,二队并着一队走,数头一共三百六,数脚一共八百九。”猎手有(
275
)人,狗有(
85
)只。
答案:2 275 85
解析:
设猎手有$x$人,狗有$y$只。
根据题意可列方程组:
$\begin{cases}x + y = 360\\2x + 4y = 890\end{cases}$
由第一个方程得:$x = 360 - y$
将$x = 360 - y$代入第二个方程:
$2(360 - y) + 4y = 890$
$720 - 2y + 4y = 890$
$2y = 170$
$y = 85$
则$x = 360 - 85 = 275$
猎手有275人,狗有85只。
3. 在“绿化校园”活动中,六年级学生和二年级学生共120名,一起给树浇水。1名六年级学生提2桶水,2名二年级学生合提1桶水。两个年级的学生共提180桶水。二年级有(
40
)名学生。
答案:3 40
解析:
设二年级有$x$名学生,则六年级有$(120 - x)$名学生。
二年级学生共提水$\frac{x}{2}$桶,六年级学生共提水$2(120 - x)$桶。
根据题意可列方程:$\frac{x}{2} + 2(120 - x) = 180$
解方程:
$\begin{aligned}\frac{x}{2} + 240 - 2x &= 180\\frac{x}{2} - 2x &= 180 - 240\\-\frac{3x}{2} &= -60\\x &= 40\end{aligned}$
40
4. (2025·苏州昆山市期末)端午期间,爸爸花42元购买了一些豆沙粽和鲜肉粽,一共12个,售价如下图。豆沙粽和鲜肉粽各买了多少个?

答案:4 豆沙粽:(4×12-42)÷(4-2.5)=4(个) 鲜肉粽:12-4=8(个)
解析:
豆沙粽:$(4×12 - 42)÷(4 - 2.5)=4$(个)
鲜肉粽:$12 - 4=8$(个)
5. 亮点原创·甲、乙两人比赛射击,规定甲命中得4分,不中失2分;乙命中得5分,不中失3分。每人各射10发,结果共命中14发,结算分数时,甲比乙多10分,甲命中(
8
)发,乙命中(
6
)发。
答案:5 8 6 解析 假设甲命中10发,乙就命中14-10=4(发),甲得4×10=40(分),乙得5×4-3×(10-4)=2(分)。根据条件“甲比乙多10分”得出假设情况与真实情况相差(40-2)-10=28(分),甲每少命中1发,少4+2=6(分),乙可增加5+3=8(分),则甲少命中28÷(8+6)=2(发),即甲命中10-2=8(发),乙命中14-8=6(发)。
解析:
假设甲命中10发,则乙命中$14 - 10 = 4$发。
甲得分:$4×10 = 40$分,
乙得分:$5×4 - 3×(10 - 4) = 20 - 18 = 2$分。
此时甲比乙多$40 - 2 = 38$分,比实际多$38 - 10 = 28$分。
甲每少命中1发,少得$4 + 2 = 6$分,乙多命中1发,多得$5 + 3 = 8$分,
甲少命中次数:$28÷(6 + 8) = 2$发,
甲命中:$10 - 2 = 8$发,
乙命中:$14 - 8 = 6$发。
8;6
6. 王叔叔运输400件仪器,到达时仪器完好,每件有2元运费;如有损坏,每件损坏的仪器不仅没有运费,王叔叔还要倒赔5元。运输结束王叔叔得到660元。这次运输过程中仪器损坏了多少件?
答案:6 (400×2-660)÷(2+5)=20(件) 解析 先假设400件仪器全部安全送到,可得运费为400×2=800(元),但实际王叔叔得到660元,比全部安全送到少了800-660=140(元),又因损坏一件不仅没有运费还要倒赔5元,所以每损坏一件仪器就会少2+5=7(元),那么损坏的件数就是140÷7=20(件)。
解析:
(400×2-660)÷(2+5)=20(件)