1. 一个圆柱的底面周长是 25.12 厘米,高是 4 厘米,这个圆柱的侧面积是(
100.48
)平方厘米,表面积是(
200.96
)平方厘米,体积是(
200.96
)立方厘米。
答案:1.100.48 200.96 200.96
解析:
侧面积:$25.12×4 = 100.48$平方厘米;
底面半径:$25.12÷3.14÷2 = 4$厘米;
底面积:$3.14×4^{2}=50.24$平方厘米;
表面积:$100.48 + 50.24×2=200.96$平方厘米;
体积:$50.24×4 = 200.96$立方厘米。
100.48;200.96;200.96
2. 把一个底面积是 $15 \mathrm{ cm}^2$、高是 $6 \mathrm{ cm}$ 的圆锥形橡皮泥捏成一个圆柱。若这个圆柱的高是 $6 \mathrm{ cm}$,则底面积是(
5
)$\mathrm{ cm}^2$;若高是 $2 \mathrm{ cm}$,则底面积是(
15
)$\mathrm{ cm}^2$。
答案:2.5 15
解析:
圆锥体积:$\frac{1}{3}×15×6 = 30\,\mathrm{cm}^3$
当圆柱高为$6\,\mathrm{cm}$时,底面积:$30÷6 = 5\,\mathrm{cm}^2$
当圆柱高为$2\,\mathrm{cm}$时,底面积:$30÷2 = 15\,\mathrm{cm}^2$
5;15
3. 如图,给一个圆柱形管道部件表面喷漆,它高 20 厘米、厚 4 厘米,底面大圆半径为 10 厘米。需要喷漆的面积是(
2411.52
)平方厘米,它的体积是(
4019.2
)立方厘米。
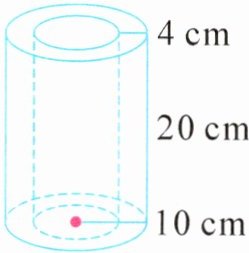
答案:3.2411.52 4019.2 解析 由题图可知,需要喷漆的面积就是大圆柱的侧面积和里面小圆柱的侧面积及上下底面圆环的面积之和,即为3.14×(2×10)×20+3.14×(10-4)×2×20+3.14×[10²-(10-4)²]×2=2411.52(平方厘米);这个管道部件的体积就是大圆柱和小圆柱的体积差,即为3.14×10²×20-3.14×(10-4)²×20=4019.2(立方厘米)。
解析:
喷漆面积:$3.14×(2×10)×20 + 3.14×(10 - 4)×2×20 + 3.14×[10^{2}-(10 - 4)^{2}]×2 = 2411.52$平方厘米
体积:$3.14×10^{2}×20 - 3.14×(10 - 4)^{2}×20 = 4019.2$立方厘米
4. 一种机器零件(如图),圆锥部分和圆柱部分的体积比是(
A
)。

A.$1 : 6$
B.$1 : 4$
C.$1 : 3$
D.$1 : 9$
答案:4.A
解析:
设圆柱和圆锥的底面半径为$r$。
圆柱体积:$V_1=\pi r^2×6 = 6\pi r^2$
圆锥体积:$V_2=\frac{1}{3}\pi r^2×3=\pi r^2$
体积比:$V_2:V_1=\pi r^2:6\pi r^2 = 1:6$
A
5. (2025·镇江润州区期末)一个圆柱形水池,底面直径是 20 米,深 2 米。
(1) 在水池的侧面和底面抹上水泥,抹水泥部分的面积是多少平方米?
(2) 水池内最多能蓄水多少吨? (每立方米水重 1 吨)
答案:5.(1)3.14×(20÷2)²+3.14×20×2=439.6(平方米)
(2)3.14×(20÷2)²×2=628(立方米)
628×1=628(吨)
水池内最多能蓄水628吨。
6. (宿迁泗洪县期末改编)如图甲,妈妈榨了一大杯西瓜汁,倒入乙杯中,可以倒满(
C
)杯。(杯子的壁厚忽略不计)

A.3
B.6
C.9
D.15
答案:6.C
解析:
甲杯半径:$8÷2 = 4\,\mathrm{cm}$
甲杯体积:$\pi×4^2×15=240\pi\,\mathrm{cm}^3$
乙杯半径:$8÷2 = 4\,\mathrm{cm}$
乙杯体积:$\frac{1}{3}×\pi×4^2×5=\frac{80}{3}\pi\,\mathrm{cm}^3$
可倒杯数:$240\pi÷\frac{80}{3}\pi = 9$
C
7. 如图,有一个圆柱形滚筒刷,它的底面直径是 6 厘米、长是 2 分米,它滚动 10 周刷过的墙面面积是多少平方厘米?

答案:7.2分米=20厘米 3.14×6×20×10=3768(平方厘米) 解析 要求滚动10周刷过的墙面面积,只要先求滚动一周刷过的面积,就是这个圆柱形滚筒刷的侧面积,然后再乘10即可,即3.14×6×20×10=3768(平方厘米)。
解析:
2分米=20厘米
$3.14×6×20×10=3768$(平方厘米)
8. 新素养 几
何直观 将右图中的这个容器倒过来后,水面的高度是(
11
)厘米。

答案:8.11 解析 容器倒过来时,原来圆柱部分的水高度不变,是23-18=5(厘米),圆锥部分高18厘米的水倒入圆柱,水的高度变为18÷3=6(厘米),合起来是5+6=11(厘米)。
解析:
23-18=5(厘米)
18÷3=6(厘米)
5+6=11(厘米)
11
9. 一个圆锥的底面周长是 18.84 厘米,从圆锥的顶点沿高将它切成两半后,表面积之和比原来增加了 24 平方厘米。原来圆锥的体积是多少立方厘米?
答案:9.18.84÷3.14=6(厘米) 24÷2×2÷6=4(厘米)
$\frac{1}{3}×3.14×(6÷2)²×4=37.68($立方厘米)
解析 根据这个圆锥的底面周长是18.84厘米,可求出它的底面直径是18.84÷3.14=6(厘米),切开后,表面积之和比原来增加了两个等腰三角形的面积,等腰三角形的底等于圆锥的底面直径,高等于圆锥的高,因此圆锥的高为24÷2×2÷6=4(厘米),圆锥的体积就是$\frac{1}{3}×3.14×(6÷2)²×4=37.68($立方厘米)。