1. 一根圆柱形钢材的底面周长是18.84厘米,高是6厘米。将它熔铸成底面积是9.42平方厘米的圆锥,这个圆锥的高是(
54
)厘米。
答案:1.54 解析·根据圆柱的底面周长,可求出它的底面半径是18.84÷3.14÷2=3(厘米),则圆柱的体积是3.14×$3^2$×6=169.56(立方厘米),将圆柱熔铸成圆锥,体积不变,那么圆锥的高就是169.56×3÷9.42=54(厘米)。
解析:
圆柱底面半径:$18.84÷3.14÷2 = 3$(厘米)
圆柱体积:$3.14×3^2×6 = 169.56$(立方厘米)
圆锥的高:$169.56×3÷9.42 = 54$(厘米)
54
2. 亮点原创 一个蛋筒冰淇淋近似形状如图(单位:厘米),每立方厘米冰淇淋重0.8克,这个蛋筒冰淇淋重(
97.968
)克。(蛋筒的质量与厚度忽略不计)

答案:2.97.968
解析:
冰淇淋体积为上部圆锥与下部圆锥体积之和。
上部圆锥:底面直径6cm,半径$ r = 3 \, \mathrm{cm} $,高$ h_1 = 3 \, \mathrm{cm} $,体积$ V_1 = \frac{1}{3} \pi r^2 h_1 = \frac{1}{3} × \pi × 3^2 × 3 = 9\pi \, \mathrm{cm}^3 $。
下部圆锥:底面半径$ r = 3 \, \mathrm{cm} $,高$ h_2 = 10 \, \mathrm{cm} $,体积$ V_2 = \frac{1}{3} \pi r^2 h_2 = \frac{1}{3} × \pi × 3^2 × 10 = 30\pi \, \mathrm{cm}^3 $。
总体积$ V = V_1 + V_2 = 9\pi + 30\pi = 39\pi \approx 39 × 3.14 = 122.46 \, \mathrm{cm}^3 $。
质量:$ 122.46 × 0.8 = 97.968 \, \mathrm{克} $。
97.968
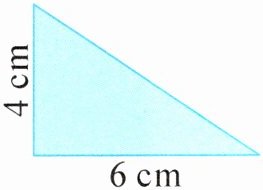
3. 有一个直角三角形(如图),分别绕它的两条直角边所在的直线旋转一周,可以形成两个圆锥,这两个圆锥的体积相差(
50.24
)立方厘米。
答案:3.50.24
解析:
当以4cm直角边为轴旋转时,圆锥底面半径$r=6\space\mathrm{cm}$,高$h=4\space\mathrm{cm}$,体积$V_1=\frac{1}{3}\pi r^2h=\frac{1}{3}×3.14×6^2×4=150.72\space\mathrm{cm}^3$;当以6cm直角边为轴旋转时,圆锥底面半径$r=4\space\mathrm{cm}$,高$h=6\space\mathrm{cm}$,体积$V_2=\frac{1}{3}\pi r^2h=\frac{1}{3}×3.14×4^2×6=100.48\space\mathrm{cm}^3$。体积差为$150.72 - 100.48=50.24\space\mathrm{cm}^3$。
50.24
4. (1)将一个圆锥的底面直径和高都扩大到原来的3倍,体积扩大到原来的(
D
)倍。
A. 6
B. 9
C. 18
D. 27
(2)将一个圆柱削成一个最大的圆锥,削去部分的体积是圆锥体积的(
D
),削去部分的体积是圆柱体积的(
C
)。
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{2}{3}$
D. 2倍
(3)一个圆柱、正方体和圆锥的底面积相等,高也相等,下面说法不正确的是(
B
)。
A. 圆锥的体积是正方体体积的$\frac{1}{3}$
B. 圆锥的体积是正方体体积的3倍
C. 圆锥的体积比圆柱的体积小$\frac{2}{3}$
答案:4.(1)D (2)D C 解析·把一个圆柱削成一个最大的圆锥,这个圆锥的体积是圆柱体积的$\frac {1}{3}$,削去部分的体积是这个圆柱体积的$\frac {2}{3}$,削去部分的体积是圆锥体积的$\frac {2}{3}$÷$\frac {1}{3}$=2倍。(3)B
5. 一个密封的沙漏,上、下都是圆锥形,底面直径都是12厘米,高都是10厘米。该沙漏下面的圆锥中装满了沙子,将沙漏倒置(如图),如果每分钟向下漏20立方厘米的沙子,那么这些沙子经过(
18.84
)分钟可以全部漏完。
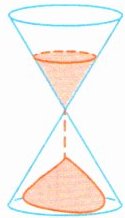
答案:5.18.84 解析·根据题意可先求出沙漏中沙子的体积,再除以沙子的流速就可求出全部漏完需要的时间,即3.14×$(12÷2)^2$×10×$\frac {1}{3}$÷20=18.84(分)。
解析:
3.14×$(12÷2)^2$×10×$\frac{1}{3}$÷20=18.84(分)
6. (2025·苏州昆山市期末)一个圆锥形的沙堆,底面周长为18.84米,高为2米。用这堆沙子去铺填一个长7.5米、宽4米的长方体沙坑,铺的厚度是多少厘米?
答案:6.18.84÷3.14÷2=3(米) $\frac {1}{3}$×3.14×$3^2$×2=18.84(立方米) 18.84÷(7.5×4)=0.628(米) 0.628米=62.8厘米
7. 一个圆柱和一个圆锥的底面积之比是$1:2$,体积之比是$5:4$。如果圆柱高30厘米,那么圆锥高(
36
)厘米;如果圆锥高30厘米,那么圆柱高(
25
)厘米。
答案:7.36 25 解析·根据圆柱和圆锥的底面积之比是1:2,体积之比是5:4,可求出圆柱和圆锥高之比为(5÷1):(4×3÷2)=5:6。如果圆柱高30厘米,那么圆锥高30÷5×6=36(厘米);如果圆锥高30厘米,那么圆柱高30÷6×5=25(厘米)。
解析:
设圆柱底面积为$S_1$,圆锥底面积为$S_2$,圆柱体积为$V_1$,圆锥体积为$V_2$,圆柱高为$h_1$,圆锥高为$h_2$。
已知$\frac{S_1}{S_2}=\frac{1}{2}$,$\frac{V_1}{V_2}=\frac{5}{4}$。
圆柱体积公式$V_1 = S_1h_1$,圆锥体积公式$V_2=\frac{1}{3}S_2h_2$,则$\frac{V_1}{V_2}=\frac{S_1h_1}{\frac{1}{3}S_2h_2}=\frac{3S_1h_1}{S_2h_2}$。
将$\frac{S_1}{S_2}=\frac{1}{2}$,$\frac{V_1}{V_2}=\frac{5}{4}$代入得:$\frac{5}{4}=\frac{3×1× h_1}{2× h_2}$,化简得$\frac{h_1}{h_2}=\frac{5}{6}$。
当圆柱高$h_1 = 30$厘米时,$\frac{30}{h_2}=\frac{5}{6}$,解得$h_2=36$厘米。
当圆锥高$h_2 = 30$厘米时,$\frac{h_1}{30}=\frac{5}{6}$,解得$h_1=25$厘米。
36;25
8. 新趋势
推导探究 如图,圆柱形容器和圆锥形容器的高和底面直径都等于球的直径,将球缓慢放进装满水的圆柱形容器后,圆柱形容器中剩下的水刚好可以装满圆锥形容器。请你推导球的体积公式。
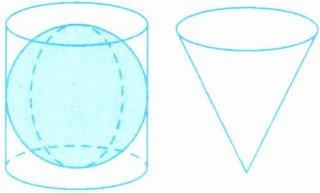
答案:8.设球的半径为r。 圆柱形容器的容积为$V_1$=$πr^2×2r=2πr^3$ 圆锥形容器的容积为$V_2$=$\frac {1}{3}πr^2×2r=\frac {2}{3}πr^3$ 则球的体积为V=$V_1$-$V_2$=$2πr^3$-$\frac {2}{3}πr^3$=$\frac {4}{3}πr^3$ 所以球的体积公式为V=$\frac {4}{3}πr^3$。