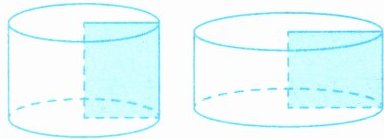
1. (2025·泰州靖江市期末)如图,把一张长5厘米、宽4厘米的长方形纸分别绕它的长和宽旋转一周,形成两个圆柱,其中较大的圆柱的体积是(
314
)立方厘米。
答案:1. 314
解析:
绕长旋转:半径$r=4$厘米,高$h=5$厘米,体积$V_1=\pi r^2 h=\pi×4^2×5=80\pi$立方厘米。
绕宽旋转:半径$r=5$厘米,高$h=4$厘米,体积$V_2=\pi r^2 h=\pi×5^2×4=100\pi$立方厘米。
$100\pi>80\pi$,$\pi$取$3.14$,$100\pi=314$立方厘米。
314
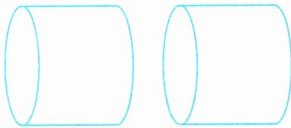
2. 如图,把一根20厘米长的圆柱形木料沿横截面切开,表面积增加了100平方厘米,原来这根木料的体积是(
1000
)立方厘米。
答案:2. 1000
解析:
将圆柱形木料沿横截面切开,表面积增加的部分为两个底面的面积。
两个底面面积之和为100平方厘米,所以一个底面面积$S = \frac{100}{2} = 50$平方厘米。
圆柱体积公式为$V=Sh$,其中$h = 20$厘米,所以体积$V=50×20 = 1000$立方厘米。
1000
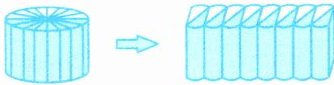
3. (淮安洪泽区期末)小强做数学实验,如图,他把一个圆柱等分后拼成一个近似的长方体,已知长方体的长是15.7分米,高是8分米,原来圆柱的体积是(
628
)立方分米。
答案:3. 628
解析:
长方体的长等于圆柱底面周长的一半,即$\frac{1}{2} × 2\pi r=\pi r$。已知长方体的长是$15.7$分米,所以$\pi r = 15.7$,$r=\frac{15.7}{\pi}\approx\frac{15.7}{3.14} = 5$分米。圆柱的高等于长方体的高,即$8$分米。圆柱体积$V=\pi r^2h\approx3.14×5^2×8 = 3.14×25×8=3.14×200 = 628$立方分米。
628
(1) 一个圆柱形油桶的体积(
B
)它的容积。
A.小于
B.大于
C.等于
答案:4. (1) B
(2) 把一个棱长为6厘米的正方体削成一个最大的圆柱,这个圆柱的体积是(
B
)立方厘米。
A.$6\pi$
B.$54\pi$
C.$36\pi$
答案:4. (2) B
解析:
圆柱底面直径为6厘米,半径$r = 6÷2 = 3$厘米,高$h = 6$厘米。体积$V=\pi r^2h=\pi×3^2×6 = 54\pi$立方厘米。B
5. 新素养 创
新意识 有一种圆形古代钱币,其直径为4厘米,厚度为2毫米,正中间的正方形缺口的边长为1厘米。把20枚这样的钱币对齐正方形缺口垒起来,则垒起来的钱币的体积是(
46.24
)立方厘米。
答案:5. 46.24
解析:
2毫米=0.2厘米
圆形古代钱币的半径:$4÷2 = 2$厘米
1枚圆形古代钱币的体积:$\pi×2^{2}×0.2-1×1×0.2$
$=3.14×4×0.2 - 0.2$
$=2.512 - 0.2$
$=2.312$立方厘米
20枚这样的钱币的体积:$2.312×20 = 46.24$立方厘米
46.24
6. 一个底面周长是188.4厘米的圆柱形玻璃鱼缸内装有适量的水。将一些水草、小石块和金鱼放到水中(水未溢出),水面上升了4厘米,这些水草、小石块和金鱼的体积一共是多少立方厘米?
答案:6. 188.4÷3.14÷2=30(厘米) 3.14×30²×4=11304(立方厘米) 解析·根据圆柱形玻璃鱼缸的底面周长,可求出底面半径为188.4÷3.14÷2=30(厘米),水草、小石块和金鱼的体积就是鱼缸内上升的4厘米高的水的体积,即为3.14×30²×4=11304(立方厘米)。
解析:
188.4÷3.14÷2=30(厘米)
3.14×30²×4=11304(立方厘米)
7. 亮点原创·甲、乙两个圆柱形水杯,底面半径的比是$2:3$,高的比是$2:1$。将甲水杯装满水后全部倒入乙水杯,乙水杯中水面距杯口1.6 cm。甲水杯的高度是(
28.8
)cm,乙水杯的高度是(
14.4
)cm。(忽略玻璃的厚度)
答案:7. 28.8 14.4 解析·根据甲、乙两个水杯的底面半径的比是2:3和高的比是2:1,得到甲、乙两个水杯的体积比为8:9。甲水杯装满水设为8份,倒入乙水杯后,距杯口还有1份的水,那么1份水的高度就是1.6cm,则乙水杯的高度为1.6×9=14.4(cm),甲水杯的高度为14.4×2=28.8(cm)。
解析:
设甲水杯底面半径为$2r$,高为$2h$,则乙水杯底面半径为$3r$,高为$h$。
甲水杯体积:$V_甲=\pi(2r)^2·2h = 8\pi r^2h$
乙水杯体积:$V_乙=\pi(3r)^2· h=9\pi r^2h$
体积比$V_甲:V_乙=8:9$。
甲水杯装满水倒入乙水杯,乙水杯内水的体积为$8\pi r^2h$,水面高度为$\frac{8\pi r^2h}{\pi(3r)^2}=\frac{8h}{9}$。
乙水杯中水面距杯口高度为$h-\frac{8h}{9}=\frac{h}{9}=1.6\,\mathrm{cm}$,解得$h=14.4\,\mathrm{cm}$。
甲水杯高度为$2h=2×14.4=28.8\,\mathrm{cm}$。
28.8
14.4
8. 新素养
推理意识 如图,一个油瓶内部深30厘米,底面内直径是10厘米。瓶里油深15厘米,把瓶盖拧紧后,使其瓶口向下倒立,这时油深25厘米。油瓶的容积是多少毫升?
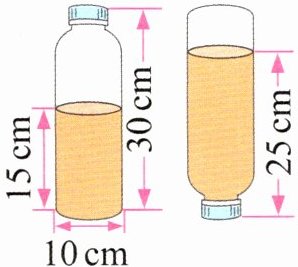
答案:8. 3.14×(10÷2)²×(30-25+15)=1570(立方厘米) 1570立方厘米=1570毫升 解析·因为油瓶的大小和形状没有发生变化,油瓶里的油也没有发生变化,所以倒置前后油的体积是相同的,空余部分的体积也是相同的,因此这个油瓶的容积=油的体积十空余部分的体积,把倒置前油瓶里的油的体积和倒置后油瓶里空余部分的体积相加,就可以求出这个油瓶的容积。
解析:
3.14×(10÷2)²×(30-25+15)=1570(立方厘米)
1570立方厘米=1570毫升