2026年同步练习江苏九年级数学下册苏科版第78页解析答案

5. 如图，水坝的横截面为梯形 $ ABCD $，迎水坡 $ AD $ 的坡角为 $ 30^{\circ} $，背水坡 $ BC $ 的坡度为 $ 1 : 1 $，坝顶宽 $ AB $ 为 $ 4 \, \mathrm{m} $，坝高为 $ 6 \, \mathrm{m} $.
(1) 求坝底宽 $ CD $；
(2) 若不改变水坝的坡度和坝底宽 $ CD $，而要用土将这段长度为 $ 1000 \, \mathrm{m} $ 的堤坝加高 $ 0.5 \, \mathrm{m} $，问需要多少土方(精确到 $ 1 \, \mathrm{m}^3 $)?

答案：
解： (1)过点A作AE⊥CD，垂足为点E，过点B作BF⊥CD，垂足为点F

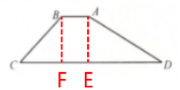
由题意可知，四边形AEFB是矩形，AB=EF=4m，BF=AE=6m，∠D=30°
在Rt△ADE中，∵∠D=30°，AE=6m
∴$DE=\sqrt 3AE= 6\sqrt 3\ \mathrm {m}$
在Rt△CBF 中，∵背水坡BC的坡度为1 ： 1，即BF：CF=1： 1
∴CF=BF=6m
∴$CD=CF+EF+DE=(10 + 6\sqrt 3)\ \mathrm {m}$
(2)增加的部分为梯形。梯形的面积：$\frac {(4- 0.5- 0.5\sqrt 3 + 4)}2×0.5×1000≈1658\ \mathrm {m^2}$
∴需要$1658\ \mathrm {m^3}$的土方。

6. 如图，一个热气球从小山东侧点 $ A $ 处开始升空，由于受西风的影响，热气球以 $ 30 \, \mathrm{m/min} $ 的速度沿与地面成 $ 75^{\circ} $ 角的方向飞行，$ 25 \, \mathrm{min} $ 后到达 $ C $ 处，此时从热气球上观测小山西侧点 $ B $ 的俯角 $ \angle DCB $ 为 $ 30^{\circ} $，则小山两侧的点 $ A $、$ B $ 间的距离为

750√2

$ \mathrm{m} $.

答案：$750 \sqrt{2}$

7. 如图是某水库的截面示意图，其中 $ AB $、$ CD $ 分别表示水库上、下游的水面，$ \angle ABC = 120^{\circ} $，$ BC = 50 \, \mathrm{m} $，则水库上、下游水面的高度差 $ h $ 为(

A.$ 25\sqrt{3} \, \mathrm{m} $
B.$ 25 \, \mathrm{m} $
C.$ 25\sqrt{2} \, \mathrm{m} $
D.$ \dfrac{50\sqrt{3}}{3} \, \mathrm{m} $

答案：A

8. 如图，梯形 $ ABCD $ 是拦水坝的横截面图，坡面 $ CD $ 的坡度是 $ 1 : \sqrt{3} $，$ \angle B = 60^{\circ} $，$ AB = 6 \, \mathrm{m} $，$ AD = 4 \, \mathrm{m} $. 求拦水坝的横截面 $ ABCD $ 的面积(精确到 $ 0.1 \, \mathrm{m}^2 $).

答案：
解：过点A作AE⊥BC，垂足为E，过点D作DF⊥BC，垂足为F

在Rt△ABE中，∵∠B=60°，AB=6m
∴BE= AB · cos 60°= 3m，$AE= AB · sin 60°= 3\sqrt 3m$
∵四边形ABCD是梯形
∴AD//EF
∵AE⊥BC，DF⊥BC
∴∠AEF=∠DFE=∠ EAD= 90°
∴四边形AEFD是矩形
∴EF=AD=4m，$DF=AE=3\sqrt 3m$
在Rt△CDF 中，坡面CD的坡度是1：$\sqrt 3$
∴$CF=\sqrt 3DF = 9m$
∴BC=BE+EF+CF=16m
∴$S_{梯形ABCD}= \frac {1}{2}(AD+ BC)×AE= 30\sqrt 3≈52.0\ \mathrm {m^2}$
答：横截面ABCD的面积为$52.0\ \mathrm {m^2}。$