13. 在锐角三角形$ABC$中,$AC = 100$,$\tan A = 1$,$\tan C = 2$. 求$BC$的长和$\triangle ABC$的面积.
答案:解:如图,作BD⊥AC,垂足为D
∵tan C=2,设DC=k,DB=2k,tan A=1
∴AD=BD=2k,但2k+k=100
∴$k=\frac {100}{3} ,$$BD=\frac {200}{3},$$BC=\sqrt{(\frac {100}{3})^2+(\frac {200}{3})^2}=\frac {100}{3}\sqrt 5$
∴$S_{△ABC}=\frac {1}{2} ×100× \frac {200}{3}=\frac {10000}{3}$
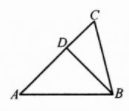
14. 如图,在$\triangle ABC$中,$\angle A = 60^{\circ}$,$\angle B = 45^{\circ}$,$AB = 8\ \mathrm{cm}$. 求$\triangle ABC$的面积(精确到$0.01\ \mathrm{cm}^2$).

答案:解:过点C作CD⊥AB,垂足为点D
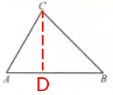
设$CD=x\ \mathrm {cm}$
在Rt△ACD中,∵$CD=x\ \mathrm {cm},$∠A=60°
∴$AD=\frac {CD}{\sqrt 3}=\frac {\sqrt 3}3x\ \mathrm {cm}$
在Rt△BCD中,∵∠B=45°
∴$BD=CD=x\ \mathrm {cm}$
∵$AB=8\ \mathrm {cm}$
∴$\frac {\sqrt 3}3x+x=8$
解得$x=12-4\sqrt 3$
∴$CD=(12-4\sqrt 3)\ \mathrm {cm}$
∴$S_{△ABC}=\frac 12×AB×CD=48-16\sqrt 3≈20.29\ \mathrm {cm^2}$
15. 如图,在$\triangle ABC$中,$AB = AC = 5$,$\sin A = \frac{24}{25}$. 求$\triangle ABC$的面积和$\cos B$的值.

答案:解:过点C作CD⊥AB,垂足为点D
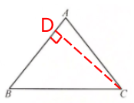
在Rt△ACD中,∵AB=AC=5,$sinA=\frac {CD}{AC}=\frac {24}{25}$
∴$CD=\frac {24}{5}$
∴$S_{△ABC}=\frac 12×AB×CD=12$
∵AC=5,$CD=\frac {24}{5}$
∴$AD=\sqrt {AC^2-CD^2}=\frac 75$
∵AB=5
∴$BD=\frac {18}{5}$
∴$BC=\sqrt {CD^2+BD^2}=6$
∴$cosB=\frac {BD}{BC}=\frac 35$