13. 求满足下列条件的锐角 $\alpha$:
(1)$-\sqrt{3}\tan\alpha+\sqrt{3}=0$;
(2)$2\cos\alpha-\sqrt{2}=0$.
答案:解:$-\sqrt 3tan α=-\sqrt 3$
tan α=1
∴α=45°
解:$cosα=\frac {\sqrt 2}2$
∴α=45°
14. 如图,在等边三角形 $ABC$ 中,点 $D$、$E$ 分别在边 $AB$、$BC$ 上,$AD=BE$,$AE$ 与 $CD$ 相交于点 $F$,$AG⊥ CD$,垂足为 $G$. 求 $\frac{AG}{AF}$ 的值.

答案:解:∵△ABC为等边三角形
∴AC=AB,∠CAD=∠B=60°
在△ADC和△BEA中
$\begin{cases}{AC=AB}\\{∠CAD=∠B}\\{AD=BE}\end{cases}$
∴$△ADC≌△BEA(\mathrm {SAS})$
∴∠ACD=∠BAE
∵∠AFG=∠ACD+∠CAE=∠BAE+∠CAE=∠BAC=60°
∴在Rt△AFG 中,$sin ∠AFG=\frac {AG}{AF}=\frac {\sqrt 3}2$
∴$\frac {AG}{AF} $的值为$\frac {\sqrt 3}2$
15. 如图,在 $\triangle ABC$ 中,$\angle B=30^{\circ}$,$P$ 是 $AB$ 上的一点,$\frac{BP}{PA}=\frac{1}{2}$,$PQ⊥ BC$,垂足为 $Q$,连接 $AQ$. 求 $\cos\angle AQC$ 的值.

答案:解:过点A作AD⊥BC,垂足为点D
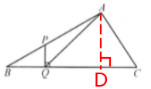
设PQ=a
∵PQ=a,∠B=30°,PQ⊥BC
∴PB=2a,$BQ=\sqrt 3a$
∵$\frac {BP}{PA}=\frac 12$
∴PA=4a,AB=PA+PB=6a
在Rt△ABD中,∵∠B=30°
∴$AD=\frac 12AB=3a,$$BD=\sqrt 3AD=3\sqrt 3a$
∴$QD=BD-BQ=3\sqrt 3a-\sqrt 3a=2\sqrt 3a$
在Rt△AQD中,∵AD=3a,$QD=2\sqrt 3a$
∴$AQ=\sqrt {AD^2+QD^2}=\sqrt {21}a$
∴$cos∠AQC=\frac {QD}{AQ}=\frac {2\sqrt 3a}{\sqrt {21}a}=\frac {2\sqrt 7}7$